Pouvez-vous s'il vous plait m'aider pour cet exercice, je n'y arrive pas du tout! MERCI!
Soit un tetraèdre SABC dans lesquel les trois faces SAB, SBC et SAC sont des triangles isocèles et rectangles en S.
Soit E, F et G les milieux respectifs du segments BC, AC, et AB.
*demontrer que SEFG est un tetraèdre régulier.
*on pose SA=a. Calculer le volume de ce tetraèdre en fonction de a.
Aider moi s'il vous plait, je ne sais pas quoi faire.
Exo de math
7 messages
- Page 1 sur 1
Bonsoir,
On pose SA = SB = SC = a
Il faut montrer que les longueurs ES, FS, GS, EF, FG, GE sont égales.
Calcul de AB :
ABS est un triangle rectangle isocèle en S. Théorème de pythagore :
SA² + SB² = AB²
2a² = AB²
donc AB = Racine(2) a
On peut montrer de manière similaire que :
BC = AC = Racine(2) a
Calcul de ES :
E est le milieu de BC.
BE = BC/2 = Racine(2)/2 a
BES est donc un triangle rectangle en E. On applique encore une fois le théorème de pythagore :
BE² + ES² = BS²
ES² = BS² - BE²
ES² = a² - a²/2 = a²/2
Donc ES = Racine(2)/2 a
On peut démontrer de la même manière que FS = GS = Racine(2)/2 a
Calcul de EF :
ABC est la base du tétraèdre SABC. On a démontré précedemment que :
AB = BC = AC = Racine(2) a
ABC est donc un triangle équilatéral de coté Racine(2) a.
On peut démontrer que EFG est également un triangle équilatéral.
Soit O le centre du triangle ABC.
E est le milieu de BC se traduit par la relation vectorielle :
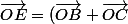 / 2)
De même F est le milieu de AC se traduit par la relation vectorielle :
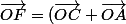 / 2)
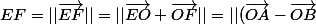/2|| = ||\vec{BA}||/2 = AB/2 = Racine(2)/2 a)
On peut démontrer de manière similaire que :
FG = GE = Racine(2)/2 a
On a donc démontré finalement que :
ES = FS = GS = EF = FG = GE = Racine(2)/2 a
SEFG est donc un tétraèdre régulier.
On pose SA = SB = SC = a
Il faut montrer que les longueurs ES, FS, GS, EF, FG, GE sont égales.
Calcul de AB :
ABS est un triangle rectangle isocèle en S. Théorème de pythagore :
SA² + SB² = AB²
2a² = AB²
donc AB = Racine(2) a
On peut montrer de manière similaire que :
BC = AC = Racine(2) a
Calcul de ES :
E est le milieu de BC.
BE = BC/2 = Racine(2)/2 a
BES est donc un triangle rectangle en E. On applique encore une fois le théorème de pythagore :
BE² + ES² = BS²
ES² = BS² - BE²
ES² = a² - a²/2 = a²/2
Donc ES = Racine(2)/2 a
On peut démontrer de la même manière que FS = GS = Racine(2)/2 a
Calcul de EF :
ABC est la base du tétraèdre SABC. On a démontré précedemment que :
AB = BC = AC = Racine(2) a
ABC est donc un triangle équilatéral de coté Racine(2) a.
On peut démontrer que EFG est également un triangle équilatéral.
Soit O le centre du triangle ABC.
E est le milieu de BC se traduit par la relation vectorielle :
De même F est le milieu de AC se traduit par la relation vectorielle :
On peut démontrer de manière similaire que :
FG = GE = Racine(2)/2 a
On a donc démontré finalement que :
ES = FS = GS = EF = FG = GE = Racine(2)/2 a
SEFG est donc un tétraèdre régulier.
Le calcul de la longueur AB nous sert dans le calcul de la longueur EF.
On a montré EF = AB /2, comme AB = on a EF =
on a EF = 
E est le milieu du segment BC donc BE = BC/2.
On a montré dans la première partie que : AB=BC=AC = ,
,
Donc BE=BC/2 =
L'application du théorème de pythagore nous amène à :
ES² = a²/2
donc ES =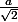 =
= 
On a montré EF = AB /2, comme AB =
E est le milieu du segment BC donc BE = BC/2.
On a montré dans la première partie que : AB=BC=AC =
Donc BE=BC/2 =
L'application du théorème de pythagore nous amène à :
ES² = a²/2
donc ES =
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 249 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
