Exo fonction et géométrie

par **davou31** » 29 Déc 2006, 19:21

bonjour, après avoir fait les 2 premières questions de cet exo, je suis totalement bloqué pourriez vous m'aider svp, merci d'avance.voilà les réponses des 2 premières questions:
1.On sait que x=AM et que AM+MI = AI = 6 cm donc x+MI = 6 cm et x = 6-MI
Donc x est forcément inférieur à 6 et puisqu'une longueur est toujours positive, alors x est supérieure à 0.
Donc on a 0 MN+2x = 12 d'où MN = 12-2x
P.S: j'espère que c'est juste...

par **yvelines78** » 29 Déc 2006, 19:39

bonjour,

1)si le rectangle existe , M varie entre A et I, N entre I et B, alors Q et P sont en C, donc 0
2)MN=AB-AM-NB
pour le calcul de MQ, utilise Thalès dans le triangle ACI ((QM) et (CI)//s)
pour cela il faut calculer d'autre parCi dans le triangle rect ACI rect en I

3)A(x)=QM*MN=xV3*(12-2x)=12xV3-2x²V3

par **mary123** » 29 Déc 2006, 20:06

Pour la question 2) pour MQ le plus rapide est d'utiliser la trigonométrie : le triangle ACB est équilatéral donc l'angle A mesure 60°

On a donc

avec

et

donc

par **lexot** » 29 Déc 2006, 20:14

Bonjour

Calcul de CI dans le triangle rectangle AIC

+

=

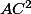
CI = 6

(MQ) // (CI) car toutes les 2 sont perpendiculaires à (AB)
Utilisation du théorème de Thalès :

=

MQ = x

A(x) = MN.MQ = 12

x - 2

Pourrais-tu me dire comment tu as inséré ta figure, sachant que j'ai cette indication, en créant une discussion :

Vous pouvez insérer des pièces jointes : non

Merci pour ta réponse

Cordialement

par **davou31** » 29 Déc 2006, 20:25

vraiment merci beaucoup pour vos réponses!pour le lien je me suis servie d'un autre forum (carremaths)car je n'y suis pas arrivé sur ce forum....

par **davou31** » 29 Déc 2006, 22:13

merci beaucoup grâce à vous j'ai pu faire les 3 premières questions et j'ai bien compris.par contre pour la 4 quand je tape la fonction et que je regarde le graphe je ne comprends pas qu'il monte si haut et du coup je peux rien conjecturer.pour la 5 j'ai calculer A(3) et j'ai trouvé 18V3.mais je ne trouve pas A(3)-A(x).pour la 6, je comprends pas...je vous remercie d'avance pour votre aide!

par **mary123** » 29 Déc 2006, 23:28

Il suffit que tu agrandisse la fenetre d'affichage de ta calculatrice et tu pourra voir la courbe en entier.

Donc

donc

Donc le maximum est atteint en 3

par **mary123** » 29 Déc 2006, 23:32

Pour la 6 il faut que MN=MQ donc

par **davou31** » 30 Déc 2006, 09:30

c'est bon j'y suis arrivé et en plus j'ai bien compris :id:!merci beaucoup à tous!

Exo fonction et géométrie

exo fonction et géométrie

Qui est en ligne