Exercice Trigonométrique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 20 Fév 2012, 14:44
par globule rouge » 20 Fév 2012, 14:44
krmn a écrit:Non je ne remarque rien

quelles valeurs peut prendre cos(x), pour tout x appartenant à R ?
-
krmn
- Membre Naturel
- Messages: 97
- Enregistré le: 30 Déc 2011, 09:43
-
 par krmn » 20 Fév 2012, 14:56
par krmn » 20 Fév 2012, 14:56
globule rouge a écrit:quelles valeurs peut prendre cos(x), pour tout x appartenant à R ?
Toutes non ?

-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 20 Fév 2012, 15:03
par Jota Be » 20 Fév 2012, 15:03
krmn a écrit:Toutes non ?

ouh non ! Pas toutes ! :hum:
cos(a)=-6, ça ne te choque pas ?
-
krmn
- Membre Naturel
- Messages: 97
- Enregistré le: 30 Déc 2011, 09:43
-
 par krmn » 20 Fév 2012, 15:05
par krmn » 20 Fév 2012, 15:05
Jota Be a écrit:ouh non ! Pas toutes ! :hum:
cos(a)=-6, ça ne te choque pas ?
Si un peu

-
krmn
- Membre Naturel
- Messages: 97
- Enregistré le: 30 Déc 2011, 09:43
-
 par krmn » 20 Fév 2012, 15:09
par krmn » 20 Fév 2012, 15:09

Je ne sais pas comment l'expliquer, avec le cercle trigo c'est plus simple.
-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 20 Fév 2012, 15:23
par Jota Be » 20 Fév 2012, 15:23
krmn a écrit:
Je ne sais pas comment l'expliquer, avec le cercle trigo c'est plus simple.
oui, exactement, cos(x) ne peut prendre que des valeurs finies de -1 à 1, pour tout x de R !
-
krmn
- Membre Naturel
- Messages: 97
- Enregistré le: 30 Déc 2011, 09:43
-
 par krmn » 20 Fév 2012, 15:35
par krmn » 20 Fév 2012, 15:35
Jota Be a écrit:oui, exactement, cos(x) ne peut prendre que des valeurs finies de -1 à 1, pour tout x de R !
Oui, je suis daccord, mais pour en revenir a la question, "exmaniner cosx = 1.5 et cosx = -3. Je dit que ce n'est pas possible car cos(x) ne peut prend que des valeurs de -1 à 1 pour tout x de R.
C'est bon ?
Merci
-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 20 Fév 2012, 15:40
par Jota Be » 20 Fév 2012, 15:40
krmn a écrit:Oui, je suis daccord, mais pour en revenir a la question, "exmaniner cosx = 1.5 et cosx = -3. Je dit que ce n'est pas possible car cos(x) ne peut prend que des valeurs de -1 à 1 pour tout x de R.
C'est bon ?
Merci
oui, donc l'ensemble des solutions est...
-
krmn
- Membre Naturel
- Messages: 97
- Enregistré le: 30 Déc 2011, 09:43
-
 par krmn » 20 Fév 2012, 15:45
par krmn » 20 Fév 2012, 15:45
Jota Be a écrit:oui, donc l'ensemble des solutions est...
cos(x) ne peut prendre que des valeurs de -1 à 1
-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 20 Fév 2012, 15:52
par Jota Be » 20 Fév 2012, 15:52
krmn a écrit:cos(x) ne peut prendre que des valeurs de -1 à 1
Oui, je sais ! :ptdr: Mais cos(x)=3/2 et cos(x)=-3
Quels x conviennent alors ?
-
krmn
- Membre Naturel
- Messages: 97
- Enregistré le: 30 Déc 2011, 09:43
-
 par krmn » 20 Fév 2012, 16:01
par krmn » 20 Fév 2012, 16:01
Jota Be a écrit:Oui, je sais ! :ptdr: Mais cos(x)=3/2 et cos(x)=-3
Quels x conviennent alors ?
Ben, j'ai pas compris là

-
Jota Be
- Membre Irrationnel
- Messages: 1422
- Enregistré le: 11 Oct 2011, 19:58
-
 par Jota Be » 20 Fév 2012, 16:38
par Jota Be » 20 Fév 2012, 16:38
krmn a écrit:Ben, j'ai pas compris là

cos(x)=3/2 est une équation dont l'ensemble de solutions est vide, et cos(x)=-3 également !
en effet,
 \in [-1;1])
-
krmn
- Membre Naturel
- Messages: 97
- Enregistré le: 30 Déc 2011, 09:43
-
 par krmn » 20 Fév 2012, 16:42
par krmn » 20 Fév 2012, 16:42
Jota Be a écrit:cos(x)=3/2 est une équation dont l'ensemble de solutions est vide, et cos(x)=-3 également !
en effet,
 \in [-1;1])
Ha ok, c'etait tout simple et logique, je ne savais pas ce que vous attendiez de moi

Merci
-
krmn
- Membre Naturel
- Messages: 97
- Enregistré le: 30 Déc 2011, 09:43
-
 par krmn » 20 Fév 2012, 17:22
par krmn » 20 Fév 2012, 17:22
Désolé, j'ai du m'absenter. Maintenant, pour la question 4, avec l'equation cos x = 0.25
Pour le placer, je le place approximativement ?
Merci
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 20 Fév 2012, 17:37
par globule rouge » 20 Fév 2012, 17:37
krmn a écrit:Désolé, j'ai du m'absenter. Maintenant, pour la question 4, avec l'equation cos x = 0.25
Pour le placer, je le place approximativement ?
Merci
Si
=\frac{1}{4})
, combien vaut

?
-
krmn
- Membre Naturel
- Messages: 97
- Enregistré le: 30 Déc 2011, 09:43
-
 par krmn » 20 Fév 2012, 17:41
par krmn » 20 Fév 2012, 17:41
globule rouge a écrit:Si
=\frac{1}{4})
, combien vaut

?
Aucune idee

-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 20 Fév 2012, 17:42
par globule rouge » 20 Fév 2012, 17:42
krmn a écrit:Aucune idee

Ben
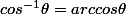
! C'est pour ça qu'on te demande de te dervir de ta calculatrice =P
-
krmn
- Membre Naturel
- Messages: 97
- Enregistré le: 30 Déc 2011, 09:43
-
 par krmn » 20 Fév 2012, 17:49
par krmn » 20 Fév 2012, 17:49
globule rouge a écrit:Ben
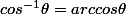
! C'est pour ça qu'on te demande de te dervir de ta calculatrice =P
Oui, Oui je suis daccord, mais pour la 4.a et b.
Comment fait on ?
Merci beaucoup
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 20 Fév 2012, 17:57
par globule rouge » 20 Fév 2012, 17:57
krmn a écrit:Oui, Oui je suis daccord, mais pour la 4.a et b.
Comment fait on ?
Merci beaucoup
non, désolée, je m'étais trompée :girl2:
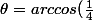)
(ça c'est pour la question 4)b)).
Pour ce qui est de la question 4)a), il te faut mettre 1/4 sur l'axe des cosinus et tracer verticalement pour placer l'image, qui est theta ici.
Excuse-moi encore :langue:
-
krmn
- Membre Naturel
- Messages: 97
- Enregistré le: 30 Déc 2011, 09:43
-
 par krmn » 20 Fév 2012, 18:08
par krmn » 20 Fév 2012, 18:08
globule rouge a écrit:non, désolée, je m'étais trompée :girl2:
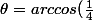)
(ça c'est pour la question 4)b)).
Pour ce qui est de la question 4)a), il te faut mettre 1/4 sur l'axe des cosinus et tracer verticalement pour placer l'image, qui est theta ici.
Excuse-moi encore :langue:
Pas de soucis

Pour la a) c'est bon, c'est deja fait. Pour la b. je n'ai pas compris comment vous avez fait.
Car, quand on place cos x = 1/4, on obtient ça (je l'ai placé approximativement):

Merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
(ça c'est pour la question 4)b)).
