Exercice

[clemiro]

bonjour, je voudrais savoir pour m'aider a faire cet exercice je ni arrive pas du tout...
alors:
ABCDA'B'C'D' est un cube de côté 4 cm, I et O sont les centres des carrés ADD'A' et ABCD.
1) Calcul de OI
a)Montrer que le triangle ACD' est équilatéral et calculer la longueur de son côté.
b)Montrer que les droites (OI) et (D'C) sont parallèles.En déduire OI.

[armor92]

Bonjour clémiro,

1) a
Pour montrer que le triangle ACD' est equilateral, on montre que :
AC=CD'=D'A

AC est la diagonale du carré ABCD (face avant du cube).
CD' est la diagonale du carré DCC'D' (face basse du cube).
D'A est la diagonale du carré ADD'A' (face gauche du cube).

La diagonale d'un carré est égale à Racine(2) * coté du carré. Ici les 3 diagonales sont égales.

Donc AC=CD'=D'A=Racine(2) * 4 cm

[armor92]

1) b)
On peut tenter un raisonnement sur les vecteurs dans l'espace à trois dimensions. Pour cela démontrons que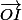 est colinéaire à .

On utilise la relation de schales :
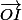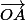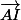= + (1)

Par hypothèse O est le centre du carré ABCD. Donc O est le milieu du segment AC.
Ceci se traduit par la relation sur les vecteurs :
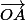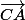= 1/2 (2)
De même I est le centre du carré ADD'A'. Donc I est le milieu du segment AD'.
Ceci se traduit par la relation sur les vecteurs :
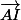= 1/2 (3)

Des relation (1) (2) et (3) on tire que :
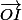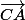= 1/2 ( + )= 1/2

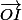colinéaire à , donc les droites (OI) et (CD') sont paralleles.

De l'égalité sur les vecteurs, on peut déduire l'égalité sur les distances.
OI = 1/2 CD'
CD' diagonale du carré face basse du cube.
Donc CD' = Racine(2) * 4 cm
D'ou
OI = Racine(2) * 2 cm