Exercice sur les Vecteurs..

[jeremy555]

Bonjour a tous!
Je suis Jeremy et j'ai vraiment besoin d'aide sur un exercice sur les vecteurs. je suis en seconde et je dois rendre le devoir demain. Le voici:
-> ->
Le Vecteur OA a pour coordonees (x-1;x+2) et le vecteur OB a pour coordonees (x+2;x+1);
x etant un reel inconnu.

A. Trouver X pour que le point O A et B soient Alignees.
B. Calculer, en fonction de x, les longeurs OA, OB et AB. Ecrire une relation que verifie X
pour que la droite (OA) et (OB) Soient perpendiculaires. En deduire les valeurs de X pour que
Cette propriete soit verifie.

Merci beaucoup, J'attends la reponse le plus rapidement possible.
Jeremy.

[Mathusalem]

A. il faut que oa ob soit colin. l un est multiple de l autre, en particulier pour 1, OA = OB. je te laisse chercher x
B. Le produit scalaire doit etre nul.

[Arnaud-29-31]

Bonsoir Jeremy,

A) O,A et aligné signifie que les vecteur et sont colinéaires, cherche donc d'abord k tel que

B) Comment est-ce que l'on calcul OA sachant qu'on a ?
(OA) et (OB) seront perpendiculaires si le produit scalaire et et est nul.

[gigamesh]

Bonsoir,
il n'y a pas de produit scalaire en seconde.

Par contre tu peux dire que (OA) et (OB) sont perpendiculaires si et seulement si OAB est rectangle en O ssi AB²= OA² + OB² et tu remplaces ces carrés de longueurs par leurs expressions en fonction de x ; il reste à résoudre l'équation.

[Arnaud-29-31]

Bonsoir,
il n'y a pas de produit scalaire en seconde.

Le produit scalaire est abordé en seconde, même si l'expression "produit scalaire" n'est pas employé ce qui me semblerait étonnant, il est forcement dit à un moment ou à un autre que deux vecteurs sont orthogonaux si xx' + yy' = 0.

[gigamesh]

Bonsoir,
non, la condition analytique d'orthogonalité n'est plus au programme de seconde depuis au moins 2002.

Pas plus que d et d' perpendiculaires ssi mm'=-1.
Au mieux, on aborde ça en DM avec une bonne classe.

[Arnaud-29-31]

Oui, tu as effectivement raison, cela n'apparaît plus dans le programme de seconde je vient de regarder ...
Cependant j'ai eu beaucoup d'élève de seconde en cours particulier l'an dernier qui avait ça dans leur cours.
(Enfin quand qqch disparaît du programme, il ne dispraît pas de declic math seconde" ^^ ceci explique peut-être cela)

Donc Jeremy, si tu as vu ça, tant mieux, sinon tant pis ^^

[jeremy555]

Merci Beaucoup mais j'ai une doute encore, l'equation pour tester la colinearite entre OA et OB me donne a la fin X^2+2=X^2+4
Est-ce que j'ai fais un erreur ou cela est comme ca?

Merci encore..

[Dinozzo13]

Pas plus que d et d' perpendiculaires ssi mm'=-1.
Au mieux, on aborde ça en DM avec une bonne classe.

Je pense pas que j'étais dans une bonne classe point de vue maths mais j'ai vue ça ainsi que la relation analytique du produit scalaire quand j'étais en 2nde, c'est-à-dire en 2007.
Ca va même peut-être t'étonner, mais j'ai vu comment résoudre une système linéaire de deux équations à deux inconnues par la méthode des déterminants (méthode que je préfère, car infaillible ^^) :++: :+++:

[Arnaud-29-31]

Tu as fais une erreur, x²+2 = x²+4 n'a aucune solution.

[Dinozzo13]

je confirme :error:

[Arnaud-29-31]

Je pense pas que j'étais dans une bonne classe point de vue maths mais j'ai vue ça ainsi que la relation analytique du produit scalaire quand j'étais en 2nde, c'est-à-dire en 2007.
Ca va même peut-être t'étonner, mais j'ai vu comment résoudre une système linéaire de deux équations à deux inconnues par la méthode des déterminants (méthode que je préfère, car infaillible ^^) :++: :+++:

Oui ca ne m'étonne pas ... je pense que même sorti du programme il est dur pour un prof de seconde de ne pas parler de produit scalaire ...

Y'a vraiment des trucs qui disparaissent du programme on ne sait vraiment pas pourquoi alors que y a des trucs qui n'ont rien a y faire ... (comme les matrices au programme de spé en ES ^^)

[Dinozzo13]

Ben, c'était du hors programme sans matrice, juste avec des déterminants, mais nous on savais pas que c'était du hors programme, car on avait déjà vu le déterminant avec des vecteurs donc voilà.
Aujourd'hui, on le sait ^^.

[jeremy555]

Pardonez moi, Est -ce que vous pouviez me montrer l' equation? Je ne trouve pas la soultion..

[jeremy555]

Bonsoir,
il n'y a pas de produit scalaire en seconde.

Par contre tu peux dire que (OA) et (OB) sont perpendiculaires si et seulement si OAB est rectangle en O ssi AB²= OA² + OB² et tu remplaces ces carrés de longueurs par leurs expressions en fonction de x ; il reste à résoudre l'équation.

Peut tu m'aider avec l'equation s'il te plait

[oscar]

Vect AB = vect AO + vect OB = - vec t OA +vect OB
=
-(x-1;x+2) + ( ( x+2;x+1)= (-x+1+x+2;-x-2+x+1) = ( 3: -1)

[gigamesh]

bonsoir,
on s'était arrêté à AB²=OA²+OB²,
qui se réécrit 3²+(-1)²=(x-1)²+(x+2)² + (x+2)² + (x+1)²
donc 10 = x² -2x +1 +x² +4x +4 + x²+4x+4 +x²+2x+1
soit 10= 4x²+8x+10
donc 4x²+8x=0 d'où x²+2x=0 x(x+2)=0
x=0 ou x+2=0
x=0 ou x=-2

x=0 donne A(-1;2) et B(2;1) (les coordonnées de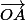 et les coordonnées de A c'est les mêmes par définition)

x=-2 donne A(-3;0) et B(0;-1)

Il reste à vérifier sur une figure (en fait deux figures, une pour le cas x=0 et une pour le cas x=-2)

[gigamesh]

Oui ca ne m'étonne pas ... je pense que même sorti du programme il est dur pour un prof de seconde de ne pas parler de produit scalaire ...

Y'a vraiment des trucs qui disparaissent du programme on ne sait vraiment pas pourquoi alors que y a des trucs qui n'ont rien a y faire ... (comme les matrices au programme de spé en ES ^^)

Pourquoi dis-tu que les matrices n'ont rien à faire en TES ?
Sais-tu ce qui motive leur utilisation dans cette série ?
As-tu déjà vu un tableau de mobilité sociale ?
clairement on est pas d'accord la-dessus !! :happy2: