Exercice sur les suites

[cmm1]

Bonjour pourriez vous m'aider svp pour cet exo:

On considère les suites (an ) et (bn) définies par leurs premiers termes a0=2 , b0=1 et, pour tout entier naturel n , par les relations de récurrence an+1= 1/5 (3an+2 bn) et bn+1= 1/5 (2 an+3 bn) .
1) (un) est la suite de terme général un=an+bn . Exprimer un+1 en fonction de un . Que peut-on en
déduire pour la suite ( un) ?
2) ( vn ) est la suite de terme général v n=an – bn . Exprimer v n+1 en fonction de v n . En déduire la
nature de la suite ( vn ) , puis l'expression de v n en fonction de n .
3) A l'aide des résultats des questions 1 et 2, exprimer maintenant an et bn en fonction de n . En
déduire que les suites (an ) et (bn) sont convergentes vers la même limite. Quelle est cette limite?

Merci d'avance

[manoa]

Salut ^^

Alors qu'as tu essayé de faire?

[cmm1]

Salut ^^

Alors qu'as tu essayé de faire?

Bon, je vais expliquer au fur et a mesure, d'abord juste la question 1

un+1 = a(n+1) + b(n+1)
= [1/5 ( 3an + 2bn)] + [1/5 ( 2an + 3bn)]
= 1/5 ( 3an + 2bn + 2an + 3bn )
=an + bn
= un

et je ne sais pas quoi conclure :s

[manoa]

Bon, je vais expliquer au fur et a mesure, d'abord juste la question 1

un+1 = a(n+1) + b(n+1)
= [1/5 ( 3an + 2bn)] + [1/5 ( 2an + 3bn)]
= 1/5 ( 3an + 2bn + 2an + 3bn )
=an + bn
= un

et je ne sais pas quoi conclure :s

tu as prouvé que pour tous n de N : u_(n+1)=u_n , cela veut dire que u_0=u_1=u_2=...=u_n=2+1=3

que peux tu en déduire ?

[cmm1]

tu as prouvé que pour tous n de N : u_(n+1)=u_n , cela veut dire que u_0=u_1=u_2=...=u_n=2+1=3

que peux tu en déduire ?

Que la suite est consatnte peut être non ? puisque on a comme vous me l'avez tres bien expliqué toujours 3. C'est cela ?

[manoa]

Que la suite est consatnte peut être non ? puisque on a comme vous me l'avez tres bien expliqué toujours 3. C'est cela ?

Oui

Plus rigoureusement tu montre que pour tout n de N : u_(n+1) - u_n=0 donc (u_n) est constante.

On passe au 2)

[cmm1]

Oui

Plus rigoureusement tu montre que u_(n+1) - u_n=0 donc (u_n) est constante.

On passe au 2)

Ah merci beaucoup, j'ai tout compris !

Alors pour le 2, j'ai :

vn = an - bn
vn+1 = a(n+1) - b(n+1)
= [1/5 ( 3an + 2bn)] - [1/5 ( 2an + 3bn)]
= 1/5 (3an + 2bn - 2an - 3bn)
= 1/5 ( an-bn)
= (an - bn ) / 5
= vn / 5

vn+1 = vn/5

Bon, a vu, la suite me parait plutot géométrique pour le quotient. Mais je ne sais pas du tout comment le montrer....

[manoa]

Bon, a vu, la suite me parait plutot géométrique pour le quotient. Mais je ne sais pas du tout comment le montrer....

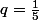
tu as prouvé que pour tous n de : c'est suffisant pour conclure que est une suite géométrique à raison et à premier terme

[cmm1]

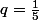
tu as prouvé que pour tous n de : c'est suffisant pour conclure que est une suite géométrique à raison et à premier terme

Ah d'accord, j'ai compris ! Merci beaucoup !

[manoa]

OK pour la suite ?

[cmm1]

OK pour la suite ?

Ici je bloque complétement ... !

[manoa]

Ici je bloque complétement ... !

le terme générale d'une suite géométrique s'écrit : ..

[cmm1]

le terme générale d'une suite géométrique s'écrit : ..

Oui, pour ça, je n'ai pas eu de soucis grace a votre aide précédente, vn = v0 * 1/5^n, c'est la formule du cours

Mais c'est pour la 3, je n'arrive pas du tout.

[manoa]

Oui, pour ça, je n'ai pas eu de soucis grace a votre aide précédente, vn = v0 * 1/5^n, c'est la formule du cours

Mais c'est pour la 3, je n'arrive pas du tout.

Si on résume ce qu'on a trouvé :



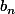
Tu peux sortir tranquillement et ^^

[cmm1]

Si on résume ce qu'on a trouvé :



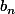
Tu peux sortir tranquillement et ^^

n'est ce pas plutot an - bn = (1/5)^n ?

[manoa]

n'est ce pas plutot an - bn = (1/5)^n ?

Oui désole, t'as raison

[cmm1]

Merci beaucoup, j'ai enfin terminé tout l'exercice grace a votre aide!
Merci !