tsukindustries a écrit:MERCI BEAUCOUP
J'ai donc changé le tableau en mettant le denominateur (x-3)?
Ca ne donnerait pas ca?
-g\left(x \right)=\frac{(4-x)(x-1)(x-2)}{x-3})
-g(x) & & - & 0 & + & 0 & - & \parallel & + & 0 & - & \end{vmatrix})
-g(x)\geq)
0 si

U

Donc
\geq g(x))
quand

U

-g(x)\leq)
0 si

U
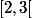
U

Donc
\leq g(x))
quand

U
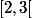
U

Nous pouvons donc dire que:
Sur l'intervalle
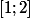
U

la courbe P est au dessus de la courbe H et
Sur l'intervalle
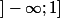
U
U

la courbe P est en dessous de la courbe H
Est ce que la colonne de trois est bon ?
Je ne suis pas certain si il faut mettre un 0 ou une double ligne sur la ligne x - 3
Partie B:
M désigne un nombre réel non nul. On désigne par

la parabole représentant la fonction

définie sur

par :
=m{x}^{2}-4mx+4m+2)
1) Montrer qu'un point M
)
appartient à la fois à l'hyperbole H et à la parabole

si, et seulement si, son abscisse x est solution de l'équation :
x-12m-2=0 (E))
 = g(x))

=0)
-(4mx(x-3))+4m(x-3)+2(x-3)-(x-4)}{x-3}=0)
+4mx-12m+2x-6-x+4=0)


x-12m-2=0)
J'ai compris par ton message qu'il fallait que je calcule
 = g(x))
pour que ca arrive a (E).
Mais comment as tu su ca? Je crois que je n'ai pas compris tres bien la question posee...
Vu que je ne comprends pas bien la question je ne vois pas comment conclure...

2)a) Vérifier que (E) est vérifiée pour x=2
x-12m-2=0)
2-12m-2=0)
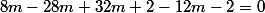
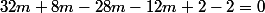
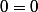
L'expression (E) est donc verifiee pour x=2
A la fin dois je mettre 0=0; N'y a t il pas une autre facon d'exprimer ceci en plus beau?b) Déterminer les réels

,

et

tels que :
x-12m-2=(x-2)({a}_{m}{x}^{2}+{b}_{m}x+{c}_{m}))
x-12m-2=(x-2)({a}_{m}{x}^{2}+{b}_{m}x+{c}_{m}))
({a}_{m}{x}^{2}+{b}_{m}x+{c}_{m}))=0)
=0)

+{x}^{2}(-7m-{b}_{m}+2{a}_{m})+x(16m+1-{c}_{m}+2{b}_{m})-12m-2+2{c}_{m}=0)
Comment puis je continuer? Merci de votre aide

Vous etes la, monsieur, devant un exercice au potentiel tres casse-luc, mais qui, en reflechissant, devient potentiellement simple =)
Je vais proceder dans l'ordre.
On t'a dit de de montrer que Fmx - gx = 0.
L'enonce te dit : Prouvez qu'un point M(x:y) Appartient a la fois a Fmx et gx, SI ET SEULEMENT SI, son abscisse X est solution de :......
Mais, quelle est la seule maniere de savoir si un point appartient a deux courbes ? On egale les courbes, et par consequent, on regarde si il y a un x pour lequel les deux fonctions ont la meme valeur. Donc, la seule maniere pour un point M(x;y) de faire partie des deux graphes a la fois, c'est qu'il satisfasse l'egalite Graphe1 = Graphe2 => Fmx = gx => Fmx - gx = 0
Apres, c'est juste rendre la forme algebrique jolie en sortant des facteurs. Mais tu as du poser fmx = gx pour trouver l'expression algebrique/la contrainte sur x, pour que M(x;y) fasse partie du graphe.
Si tu te poses la question de pourquoi est-ce qu'on se fiche de la coordonnee y, c'est simplement parce que c'est un detail : On designe une fonction quelconque f(x) = y = {expression}. En mettant debout l'egalite Fmx = gx, il est deja implicite qu'on cherche y = y, on veut que leur valeur soit identique, ce qu'il nous manque, c'est la coordonnee en x au lieu ou ca se passe. J'espere avoir ete clair.
Pour conclure tu peux dire : La maniere de trouver la contrainte sur la coordonnee x pour qu'elle donne un point appartenant aux deux graphes est de poser Fmx = gx, par consequent {developpement, blabla} On se rend compte que les deux expressions (donnee, et trouvee) coincident. Fin
2. Non, il n'y a pas de moyen plus joli. On te donne une contrainte sur x, il faut que x satisfasse l'equation .... = 0
Si tu mets 3, tu trouveras = 12 (admettons) et non pas = 0.
Tu as une equation de depart de la forme {expression} = 0
Et non pas {expression} = 3 ou 7 ou 39, mais = 0
Par consequent, en remplacant x par la valeur 2, si tu trouves 0, c'est que 2 etait une valeur qui satisfaisait la contrainte.
En remplacant par 3, tu aurais trouve 12, mais ton expression de base voulait 0, ca ne coincide donc pas...
3. Mechant si on ne s'y prend pas bien
x-12m-2=(x-2)({a}_{m}{x}^{2}+{b}_{m}x+{c}_{m}))
Il faut avoir l'oeil
La maniere tres simple d'y parvenir, c'est de ce rendre compte, qu'on a une expression au cube d'un cote, et une expression en (x-..)(x^2+...) de l'autre.
Tu peux diviser
x-12m-2)
par (x-2) (Division euclidienne)
Tu sais egalement que tu devras trouver comme reponse (puisque tu divises une puissance 3 par une puissance 1) ax^2 + bx + c
En faisant la divison euclidienne complete, tu vas avoir des vrais coefficients a, b et c, qui doivent tour a tour correspondre a Am, Bm, Cm
Si tu n'y vois pas clair, tu peux commencer ta divison euclidienne sans preter attention a l'autre cote de l'egalite :
x-12m-2)
/(x-2)
Combien de fois (x-2) dans
x-12m-2)
? il y a

fois (x-2) dans
x-12m-2)
Donc
x-12m-2)
-
)
=
x-12m-2)
Etc jusqu'a eliminer le dernier terme, et tu te retrouveras avec une reponse du genre ax^2 + bx +c , et tu peux la mettre en relation avec
)
Bonne chance !
