Exercice sur les dérivées 1èS

[Anonyme]

Bonjour! Notre prof nous a donné à faire quelques dérivées de fonctions. Je les ai déja faites, mais j'aimerais savoir si elles sont justes bien que je sache utiliser ma calculatrice pour les vérifier, j'ai peur de ne pas savoir les taper comme il faut avec les parenthèses et que l'erreur vienne de là.

1) f(x) =

-->
Posons u(x) = .
Alors u'(x) = 1/(2).

F(x) est de forme 1/u donc f '(x) = -1/(2x)

2) f(x) = -3x+1- (1/2x+1).
Je trouve f '(x)= -3 + (2/(2x+1)²)

3) f(x) = (2x-1)/(x^3)
Je trouve f '(x) = [(2x^4)-(6x^3)+3x²]/(x^6)

Merci pour votre aide =)

[uztop]

Bonjour,

attention, que vaut ?

[Anonyme]

Bonjour,

attention, que vaut ?

Si f(x) =(1/u), f'(x) = -u'/u². oO

Pour le premier résultat je trouve:

f'(x) =

[-1/(2*racinede(x))]/x

= -1/(2*racinede(x)) * 1/x

= -1/ (2*racinede(x))*x

[uztop]

oui, et est ce que tu obtiens f '(x) = -1/(2x) avec ça ?

[Anonyme]

J'ai du me tromper en simplifiant.. :hein:

En fait je trouve

[uztop]

oui c'est ça

Sinon, la 3 peut se simplifier

[Anonyme]

Et dans cette expression je ne sais plus comment on réduit la racine avec le petit x. :hum:

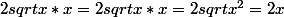
car = x

[oscar]

Bonjour

le 3e calcul n'est pas terminé

[CDuce]

salut a tous, alors pour les derivées que t'as trouvé, la deuziéme est juste les autres malheureusement non, bon commençons par la 1er.

f(x)=1/ rac(x) ,
Et bien si tu pose u(x)= rac (x) t'auras a cherché la derivée de: 1/u(x)
qui est : -u'(x)/u²(x) or u'(x)=1/2*rac(x)
alors f'(x)=-1/2*x*rac(x).

Bon alors passons a la 3eme : f(x)= (2x-1)/x^3 :
f'(x)=[2x^3-(2x-1)*3x^2]/x^6
= (3x^2-4x^3)/x^6 .

Et voila CQFD :)
J'espere que l'écriture est claire!!

[Anonyme]

salut a tous, alors pour les derivées que t'as trouvé, la deuziéme est juste les autres malheureusement non, bon commençons par la 1er.

f(x)=1/ rac(x) ,
Et bien si tu pose u(x)= rac (x) t'auras a cherché la derivée de: 1/u(x)
qui est : -u'(x)/u²(x) or u'(x)=1/2*rac(x)
alors f'(x)=-1/2*x*rac(x).

Bon alors passons a la 3eme : f(x)= (2x-1)/x^3 :
f'(x)=[2x^3-(2x-1)*3x^2]/x^6
= (3x^2-4x^3)/x^6 .

Et voila CQFD
J'espere que l'écriture est claire!!

Merci, c'est gentil :]
En tout cas,c'est juste, mais je n'arrive pas à trouver des valeurs exactes da,ns mon tableau de valeurs lorsque je veux vérifier avec ma TI82. Pourtant je connais la méthode.. :/