Exercice de maths
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
danyL
- Membre Rationnel
- Messages: 682
- Enregistré le: 03 Jan 2015, 13:29
-
 par danyL » 20 Nov 2017, 20:24
par danyL » 20 Nov 2017, 20:24
lola12968 a écrit:x-px+xpq =1
bonsoir
tu peux mettre x en facteur puis diviser par son coefficient
x (..) = 1
x = 1/ (...)
-
lola12968
- Membre Relatif
- Messages: 128
- Enregistré le: 25 Sep 2017, 21:27
-
 par lola12968 » 20 Nov 2017, 22:25
par lola12968 » 20 Nov 2017, 22:25
x en facteur :
x(pq-p) =1
-
lola12968
- Membre Relatif
- Messages: 128
- Enregistré le: 25 Sep 2017, 21:27
-
 par lola12968 » 20 Nov 2017, 23:30
par lola12968 » 20 Nov 2017, 23:30
On a donc
x=1/(pq-p)
?
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 20 Nov 2017, 23:36
par infernaleur » 20 Nov 2017, 23:36
lola12968 a écrit:x en facteur :
x(pq-p) =1
c'est faux ....
si on développe tu auras xpq-px=1 et c'est pas sa qu'on avait.
Bref c'est :
x-px+xpq =1 <=> x(1-p+pq)=1 <=> x=1/(1-p+pq)
maintenant il faut que tu trouves y.
-
lola12968
- Membre Relatif
- Messages: 128
- Enregistré le: 25 Sep 2017, 21:27
-
 par lola12968 » 21 Nov 2017, 08:20
par lola12968 » 21 Nov 2017, 08:20
(1-p)(1/(1-p+pq)) + y=1
y=-(1-p) (1/(1-p+pq)) +1
-
lola12968
- Membre Relatif
- Messages: 128
- Enregistré le: 25 Sep 2017, 21:27
-
 par lola12968 » 21 Nov 2017, 08:24
par lola12968 » 21 Nov 2017, 08:24
= (-1+p) (...
=(-1+p)/(1-p+pq) +1

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 21 Nov 2017, 08:30
par chan79 » 21 Nov 2017, 08:30
salut
tu peux simplifier l'expression de y
-
lola12968
- Membre Relatif
- Messages: 128
- Enregistré le: 25 Sep 2017, 21:27
-
 par lola12968 » 21 Nov 2017, 10:09
par lola12968 » 21 Nov 2017, 10:09
-1/(1-p+q) +1
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 21 Nov 2017, 11:36
par pascal16 » 21 Nov 2017, 11:36
pour la d)
x-px+xpq =1
x(1-p+pq)=1
je divise par (1-p+pq) (en théorie, j'ai vérifié qu'il était non nul, on peut remarquer que 1-p+pq=0 n'apporte pas de solution)
x=1/(1-p+pq)
on retrouve y ensuite
pour la e)
A(0;0)
A'(r/(r-1); 1/(1-r))
(AA') passe par l'origine, son équation réduite est du type y=ax
avec a: le coefficient directeur (YA'-YA)/(XA'-XA).
en remarquant que 1-r= -(r-1), ça se simplifie.
-
Tiruxa47
- Membre Relatif
- Messages: 343
- Enregistré le: 14 Jan 2017, 16:03
-
 par Tiruxa47 » 21 Nov 2017, 18:06
par Tiruxa47 » 21 Nov 2017, 18:06
lola12968 a écrit:-1/(1-p+q) +1
Attention c'est faux, on ne peut pas simplifier ainsi.
La seule chose à faire c'est de réduire au même dénominateur
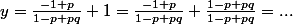
-
lola12968
- Membre Relatif
- Messages: 128
- Enregistré le: 25 Sep 2017, 21:27
-
 par lola12968 » 22 Nov 2017, 13:07
par lola12968 » 22 Nov 2017, 13:07
Pq/(1-p+pq)
-
lola12968
- Membre Relatif
- Messages: 128
- Enregistré le: 25 Sep 2017, 21:27
-
 par lola12968 » 22 Nov 2017, 13:20
par lola12968 » 22 Nov 2017, 13:20
Donc le point H aurait pour coordonnées
(1/(1-p+pq) ; Pq/(1-p+pq) )
-
lola12968
- Membre Relatif
- Messages: 128
- Enregistré le: 25 Sep 2017, 21:27
-
 par lola12968 » 22 Nov 2017, 14:08
par lola12968 » 22 Nov 2017, 14:08
Mais je ne suis pas sûr que mon calcul soit bon
?
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 22 Nov 2017, 14:32
par infernaleur » 22 Nov 2017, 14:32
Si c'est juste
-
lola12968
- Membre Relatif
- Messages: 128
- Enregistré le: 25 Sep 2017, 21:27
-
 par lola12968 » 22 Nov 2017, 14:49
par lola12968 » 22 Nov 2017, 14:49
Donc la question d est fini
Ouf
Pour la question e )
On sait que A(0;0) et que A'(r/(r-1); 1/(1-r))
(AA') passe par l'origine, son équation réduite est du type y=ax
On calcul a = (yA'-yA)/(xA'-xA)
=(1/(1-r)-0)/(r/(r-1)-0)
=(1/(1-r))/(r/(r-1))
=(1/-(r-1))/(r/(r-1))
=-1
Y=-x
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 22 Nov 2017, 15:19
par infernaleur » 22 Nov 2017, 15:19
Comprend tu pourquoi
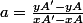
?
Sinon tu as juste à procéder ainsi (sa évite d'apprendre des formules pour rien):
ton équation est normalement du type

comme c'est une droite.
Comme elle passe par le point (0,0).
On a
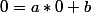
d'où
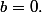
C'est donc pour sa que l'équation est réduite à y=ax
Ensuite pour trouver a on fait la même chose mais utilise le fait que la droite passe par A'=(r/(r-1); 1/(1-r))
Donc on a
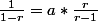
Et on trouve a=-1/r
Modifié en dernier par
infernaleur le 22 Nov 2017, 15:22, modifié 1 fois.
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 22 Nov 2017, 15:21
par infernaleur » 22 Nov 2017, 15:21
lola12968 a écrit:Donc la question d est fini
Ouf
Pour la question e )
On sait que A(0;0) et que A'(r/(r-1); 1/(1-r))
(AA') passe par l'origine, son équation réduite est du type y=ax
On calcul a = (yA'-yA)/(xA'-xA)
=(1/(1-r)-0)/(r/(r-1)-0)
=(1/(1-r))/(r/(r-1))
=(1/-(r-1))/(r/(r-1))
=-1/r
Y=-x
tu as fait une petite erreur tu as oublié le r
-
lola12968
- Membre Relatif
- Messages: 128
- Enregistré le: 25 Sep 2017, 21:27
-
 par lola12968 » 22 Nov 2017, 15:26
par lola12968 » 22 Nov 2017, 15:26
Oui j'ai compris
Donc y=(-1/r)x
-
lola12968
- Membre Relatif
- Messages: 128
- Enregistré le: 25 Sep 2017, 21:27
-
 par lola12968 » 22 Nov 2017, 15:47
par lola12968 » 22 Nov 2017, 15:47
Mais ça me semble bizard
-
lola12968
- Membre Relatif
- Messages: 128
- Enregistré le: 25 Sep 2017, 21:27
-
 par lola12968 » 22 Nov 2017, 15:58
par lola12968 » 22 Nov 2017, 15:58
Non c'est bon !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités