Exercice maths Spé Terminale

[sarahdvz66]

Bonjour à tous, dû à des absences, je n'étais pas présent sur ce chapitre et j'ai du mal à faire cet exercice, merci bcp à ceux qui voudront m'aider

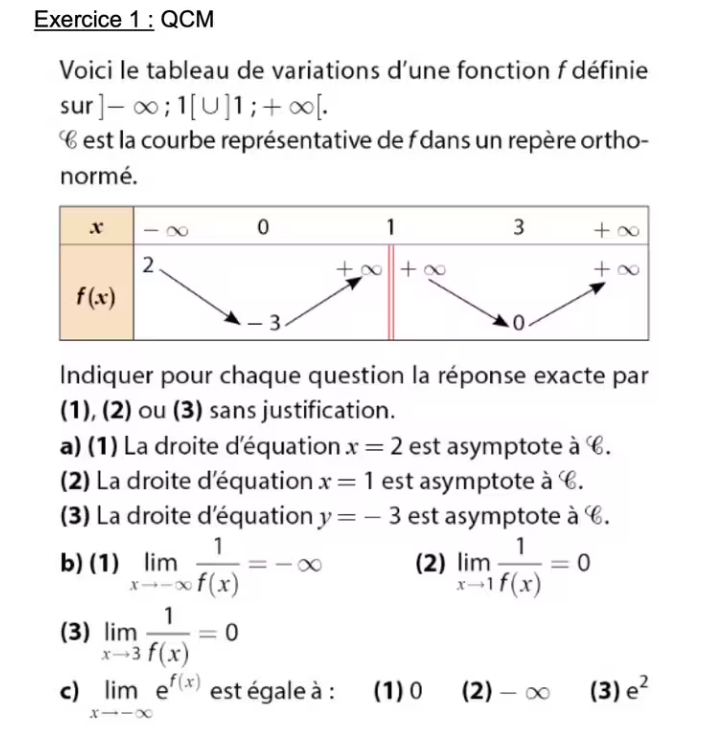
Voici le tableau de variations d'une fonction f définie
sur] - infini ; 1 [U] 1; + infini [
C est la courbe représentative de f dans un repère ortho-normé.

tableau :

x / -infini 0 1 3 +infini
------------------------------------------------------------------------------
f(x) / 2 +infini // +infini +infini
-> -> // -> ->
-3 // 0


(j'espère que vous le comprenais, je ne peux pas faire monter ou descendre les flèches mais par exemple c'est décroissant de 2 à -3 et croissant de -3 à +infini et décroissant de +infini à 0 et croissant de 0 à +infini)

Indiquer pour chaque question la réponse exacte par
(1), (2) ou (3) sans justification.

a)

(1) La droite d'équation x = 2 est asymptote à C.
(2) La droite d'équation x = 1 est asymptote à C.
(3) La droite d'équation y = - 3 est asymptote à C.

b)
(1) lim 1/f(x) = -infini
x-->-infini

(2) lim 1/f(x) = 0
x-->1

(3) lim 1/f(x) = 0
x-->3

c)
lim e exposant f(x) est égale à :
x-->-infini

(1) 0
(2) -infini
(3) e exposant 2

mes réponses :

a) (1)faux (2) vrai (3) vrai
b) (1) faux (2) vrai (3) vrai
c) (1) vrai (2) faux (3) faux

si vous pouviez m'expliquer pour chaque réponse svp

merci à tous

[sarahdvz66]

quel extension est autorisé pour mettre une pièce jointe ? pdf, doc etc absolument tout est refusé

[sarahdvz66]

file:///Users/yanis/Desktop/exo%2011.html

ce lien pour voir le tableau

[vam]

Bonjour

tu as des sites comme ça pour héberger ton image et ensuite tu suis les explications pour choisir ce que tu mets ici
https://postimages.org/fr/

[sarahdvz66]

d'accord, merci voici le lien du tableau : https://postimg.cc/xNQ2F73Q




vam edit

[catamat]

Bonjour

mes réponses :

a) (1)faux (2) vrai (3) vrai
b) (1) faux (2) vrai (3) vrai
c) (1) vrai (2) faux (3) faux

Plusieurs erreurs
a)(3)
b)(3)
c)(1) et (3)

Ce qui serait bien c'est de comprendre pourquoi ces réponses étaient fausses !

[sarahdvz66]

oui effectivement si vous pouviez m'expliquer !

[catamat]

Bon pour les asymptotes

On a une asymptote "horizontale" d'équation y=a si et seulement si la limite de f est égale à a lorsque x tend vers plus l'infini ou moins l'infini.
Dans notre exemple on a donc y=2.

On a une asymptote "verticale" d'équation x=a si et seulement si la limite de f est infinie lorsque x tend vers a, par valeurs inférieures ou supérieures.
Ici on a donc x=1

Donc seule la réponse b est vraie.

Pour les limites (ce sont des fonctions composées)

Pour les trois premières c'est f suivie de la fonction inverse
la limite de f en moins l'infini est égale à 2, la fonction inverse en 2 a pour limite 1/2, donc 1/f a pour limite 1/2. Réponse fausse

En 1 la limite de f est infinie, la fonction inverse à l'infini a pour limite 0, donc 1/f a pour limite 0. Réponse vraie

En 3 la limite de f est 0+, la fonction inverse en 0+ a pour limite plus l'infini, donc la limite de 1/f est plus l'infini. Réponse fausse

Pour la dernière c'est f suivie de la fonction exponentielle
la limite de f en moins l'infini est égale à 2, la limite de la fonction exponentielle en 2 est e² donc la limite demandée est e².

[sarahdvz66]

d'accord merciii beaucoup