EXERCICE LIMITE ET CONTINUITE

[henri078]

Bonjour, je ne parviens pas à saisir un point dans un exercice , j'aurais besoin d'un petit coup de main :


EXO
On considère la fonction f définie sur [0;+;)[ par*: f(x) = -x³+6x²-10x+8. On note C sa courbe représentative dans un repère orthonormé (O; I; J) :


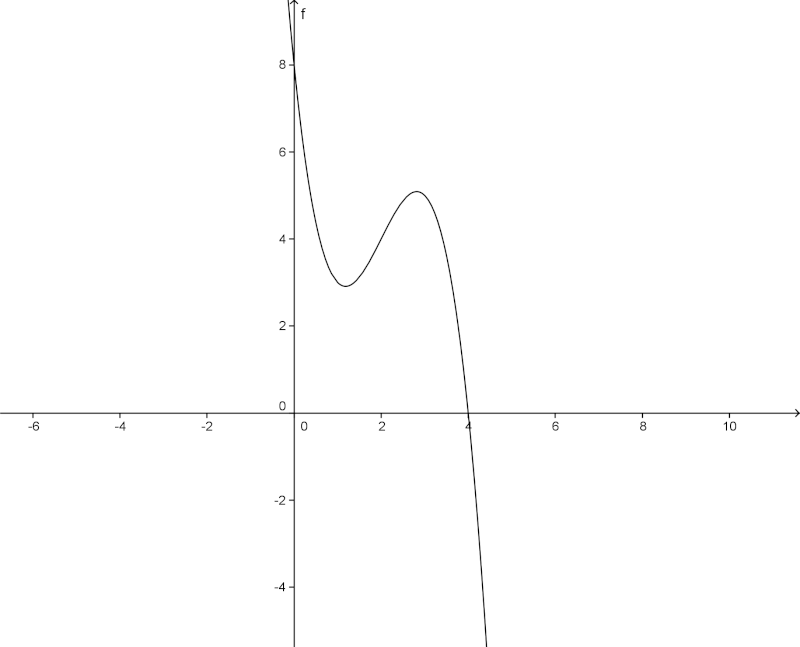
Pour tout réel x de l'intervalle ]0;4[, on note M le point de C de coordonnées (x , f(x)), P le point de coordonnées (x ; 0) et Q le point de coordonnées (0 ; f(x)),
1, Démontrer que l'aire du rectangle OPMQ est maximale lorsque M a pour abscisse alpha , alpha étant le réel défini dans la partie A,
2 . Le point M a pour abscisse alpha . La tangente en M à la courbe C est -elle parallèle à la droite (PQ )? n rappelle que le coefficient directeur de la tangente en un point x0 est f'(x0).


2. La je suis bloqué , je ne comprends pas. Pourriez vous m'aider svp ?

[aviateur]

Bonjour
C'est un exercice type bac pour les littéraires?

[henri078]

bonjour , non c'est un exercice de mon livre de maths de ts.

[pascal16]

Sur un exo type bac qui sera bcp moins long, mais je sens que tu veux chopper tous les points :
A2
x | 0 0.7 2.3 +infini

rédige façon bac (où tu auras sans doute un "alpha" à donner à 0.01 près) :
x | 0 x1 x2 +infini

et il faudra la forme exacte de g(x1) et g(x2), perso je rajoute sa valeurs approximative car c'est plus parlant

[pascal16]

A'(x)> 0 pour x appartient à [0 ; alpha] et A'(x)< 0 pour x appartient à [alpha;+infini[

attention, le sens de tes crochets n'est pas bon pour des inégalités au sens strict

pour la dernière
la notion de 'pente' ayant un peu de mal à revenir dans les programmes, je passe par les vecteurs :
-> un vecteur directeur de la tangente est (1, f'(alpha))
-> un vecteur directeur de (QP) est (1;-1)

[rcompany]

les pentes de T et PQ sont et

On montre facilement que la différence entre les deux pentes est égale à car donc PQ et T sont parallèles.

[henri078]

Et comment puis-je démonter que la tengente T est égale a f'(alpha)
et que le droite PQ est égale a -f(alpha) / alpha ?
merci pour votre aide.

[pascal16]

j'ai une erreur dans mon (PQ) en effet
entre P et Q : on augmente de α sur l'axe x et on diminue de -f(α) sur l'axe y.
donc (α ;-f(α) ) est un vecteur directeur de (PQ),(1;-f(α) /α) en est un autre (cf le post de rcompany)


Et comment puis-je démonter que la tangente T est égale a f'(alpha) <-- attention T est une droite, f'(alpha) un nombre

par définition la tangente à une courbe f en un point d’abscisse a pour équation réduite :
y= f(a)+f'(a)(x-a)
un vecteur directeur de cette droite est (1; f'(a))