Salut,
Alors tu ferais comment?
Exercice étude de fonction
3 messages
- Page 1 sur 1
Re: Exercice étude de fonction
le reste n'est que du bla bla, on peut parfaitement résoudre le problème avec ça :
Soit A et B 2 nombres > 0.
Soit f(t) = A*t^2 + B*t^-2
Démontrez que je le minimum de cette fonction est 2*sqrt(AB)
-> domaine de définition
-> comparer f(t) et f(-t), conclure sur le fait qu'on peut étudier seulement t>0
-> limites en 0+ et +oo
-> conclusion sur la particularité du point où elle atteint son minimum
-> dérivée
-> un peu de calcul avec des racine quatrièmes
-> conclusion finale
Soit A et B 2 nombres > 0.
Soit f(t) = A*t^2 + B*t^-2
Démontrez que je le minimum de cette fonction est 2*sqrt(AB)
-> domaine de définition
-> comparer f(t) et f(-t), conclure sur le fait qu'on peut étudier seulement t>0
-> limites en 0+ et +oo
-> conclusion sur la particularité du point où elle atteint son minimum
-> dérivée
-> un peu de calcul avec des racine quatrièmes
-> conclusion finale
Re: Exercice étude de fonction
Salut,
D'un autre coté, si on a un peu de "jugeote calculatoire" et qu'on a parfaitement compris l'astuce de la "mise sous forme canonique" des trinômes du second degré, un truc qui peut venir à l'esprit, c'est d'écrire directement que, pour tout réel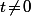 , on a :
, on a :
^{\!\!2}+2\sqrt{AB}<br />\geq2\sqrt{AB})
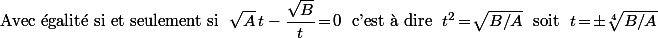
D'un autre coté, si on a un peu de "jugeote calculatoire" et qu'on a parfaitement compris l'astuce de la "mise sous forme canonique" des trinômes du second degré, un truc qui peut venir à l'esprit, c'est d'écrire directement que, pour tout réel
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
