Exercice TS coordonnées/angles

[Arnaud-29-31]

Euh non ... y'a une petite erreur.

[tite_prune]

Je crois que je me suis en effet trompée dans un igne donc
f(x)²=(1-x)²(1-x²)/4?

[Arnaud-29-31]

Oui .... Et 1-x² ca peut s'écrire comment ?

[tite_prune]

a oui! donc ca fait f(x)²=(1-x)^4/4
soit f(x)=(1-x)²/2

[Arnaud-29-31]

Aiie .... non 1-x² c'est une identité remarquable (a² - b²)

[tite_prune]

Donc c'est ( je vais y arriver un jour ^^)
f(x)²=(1-x)²(1-x²)/4
soit = (1-x)²(1-x)(1+x)/4
=(1-x)(1+x)/4
ce qui nous fait f(x)²=g(x)/4

[Arnaud-29-31]

Oui voila ... ca peut aider, nan ?? :p

[tite_prune]

désolée jme sens vraiement troooooop nul ( et j'espère que je vous embête pas trop) mais je vois pas ce que ca va donner

[Arnaud-29-31]

Trace bien ton tableau de variation pour x compris entre -1 et 1.
place les valeur g(-1) et g(1) tu verras que g(x) est toujours positif (normal, on vient de dire que c'était un carré) ensuite f(x) aussi est toujours positif donc on peut dire que

[tite_prune]

voila mon tableau:
http://img40.imageshack.us/f/tableaut.jpg/

ensuite j'en fais quoi avec f(x)?

(je m'en vais me coucher donc on continu ça demain vous avez la patiente et si vous êtes la , en tout cas merci pour tout pour le moment :we: )

[Arnaud-29-31]

Oui, et bein ensuite avec l'expression de f que je t'ai donné dans le post précédent, on voit bien que f varie comme g

[tite_prune]

A ben oui !
donc ca va être les même variations dans le tableau.
Ensuite j'ai fais la prochaine question
3)Pour quelles positions du point M l'aire A est-elle maximale?Quelle est la valeur de ce maximumu.
Donc dans le tableau on voit que -1/2 est le maximum.
et après on calcule
f(-1/2)=
je crois donc que ce point là est juste , du moins j'espère
Ensuite vient une deuxième partie :avec un angle.
On désigne la mesure en radian de l'angle .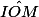

1)Démontrer que A=1/4(2sin-sin2)

2)Soit h la fonction définie sur [0;] par h(t)=2sint-sin2t
a-démontrer que , pour tout réel t de [0;], on a :h'(t)=2(1-cost)(1+2cost)
b)en déduire le tableau des variations de la fonction h

3)Retrouver les résultats de la question3) du précédent .

voilà la fin de mon problème.

j'ai une idée pour la question 1:

A = (1/2).IH.HM
A = (1/2).(IO+OH).(OM.sin )
A = (1/2).(IO+OM.cos ).(OM.sin)
A = (1/2).(1+cos(-)).sin(-)
A = (1/2).(1-cos()).sin()
A = (1/2).( sin() - cos().sin() )
A = (1/4).( 2.sin() - 2.cos().sin() )
A = (1/4).( 2.sin() - sin(2.) )

[tite_prune]

Je up mon post pour qu'il ne coule pas jusqu'à votre retour

[Arnaud-29-31]

J'ai l'impression qu'il y a une petit erreur dans le calcul de f(-1/2).
Sinon tu peux utiliser l'expression de f(x) que l'on a au début.

Ensuite pour la suite, ce que tu as écris ne m'a pas l'air très juste (on ne sait en plus pas trop si tu parles de longueurs ou de vecteurs).
Le mieux est d'exprimer cos() et sin() en fonction de x.

[tite_prune]

alors au final je trouve 3

[Arnaud-29-31]

Non, on doit trouver

[tite_prune]

A ben après beaucoup de recherche j'ai enfin réussi à trouver le même résultat.
Je peux poster le developement si vous voulez.

Sinon après pour la partie 2 je vois pas du tout comment faire :triste:
je pensais que j'étais sur la bonne voie mais en faite pas du tout ^^

[Arnaud-29-31]

Tu as exprimé cos() et sin() ? Si ton schéma est bien fait ca saute aux yeux.

[tite_prune]

ben je vois pas comment exprimer le cos et le sin vu que si on change le pont M de place le cosinus et le sinus varient aussi

[Arnaud-29-31]

C'est pour ça que l'on a une variable qui est x, on va exprimer le cos et le sin en fonction de x.