Examen, la loi binomiale et le binome de Newton

[jocaron02]

Bonjour,

Je me permets de venir demander votre aide car, malgré mes recherches, je ne trouve aucune réponse à ces questions (en tout cas, aucune réponse n'est assez bonne pour le prof)...

Je ne demande pas forcément les réponses, mais au moins une petite indication, cela m'aiderait grandement ! Voici les trois questions où je bloque :

• Explique pourquoi la loi Binomiale est une forme du binôme de Newton?
• Quelle est la formule de la loi normale réduite? Explique la différence de cette loi avec la loi normale?
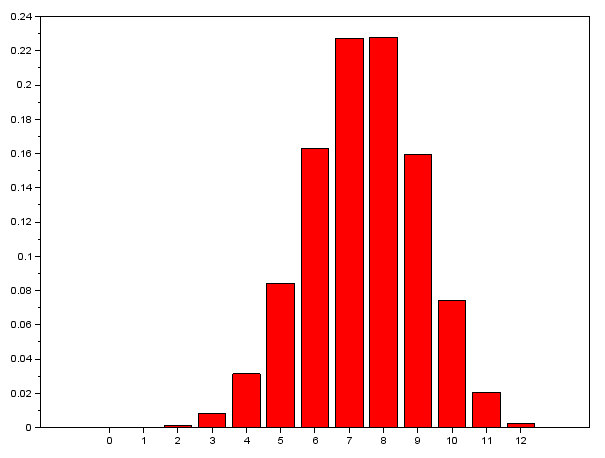
• Un questionnaire est proposé à l'examen et comporte 12 questions, 7 en français et 5 en math. Si tu as étudié 70% de la matière de français et seulement 50% de celle de math, quelle sera la probabilité de réussir l'examen avec au moins 90% ?

En vous remerciant par avance.

[pascal16]

une façon :
Explique pourquoi la loi Binomiale est une forme du binôme de Newton
en faisant un arbre de proba qui recense tous les chemins possibles d'un coté
(a+b)^n = (a+b)(a+b)...(a+b) et de remarqué que le nombre de chemin où a est la puissance n est aussi le nombre de chemins qui conduisent à n réussites du la loi binomiale.

Quelle est la formule de la loi normale centrée réduite : voir le bouquin : Y=(X-m)/sigma
Je ne sais pas si le changement de variable dans les intégrales est au programme, sinon, on ne démontre pas.

arbre et formule des probabilités totales, qui de toute façon donne un résultat entre 50 et 70 % (hors considération de chance ou de pif sur un QCM).

[jocaron02]

Tout d'abord, merci pour votre réponse explicité, j'ai déjà bien pu comprendre la première.

Pour la deuxième, j'ai en effet donné la formule de la première partie de la question, mais c'est surtout à cette partie que je bloque : "Explique la différence de cette loi avec la loi normale?"

Pour la troisième, je suis tout à fait d'accord mais il faut une réussite de minimum 90%, je dois quand même donner la probabilité. Je sais qu'il y a 12 questions, il faut que je fasse 12 ou 11 (car 10 < 90%). Le prof m'a dit que ça ne se faisait pas par la loi binomiale mais plutôt avec un peu de réflexion. C'est là que je suis totalement perdu.

[beagle]

ah tu veux 11 ou 12?
alors 7+5 =12
7+4=11
6+5=11

[jocaron02]

C'est plus complexe, il faut un pourcentage.

Quelqu'un m'a donné la réponse, mais je ne comprends pas comment il calcule ce p(raté 0) et ce p(raté 1) :

[beagle]

"C'est plus complexe, il faut un pourcentage."

c'est plus complexe que la solution sus-jaccente
puisque tout réussir il n' ya qu'un seul choix pour les 7 et 1 seul choix pour les 5, nous sommes d'accord


mais retour au binomial
pour 6+5 car:
réussir 6 sur 7, il y a C(6,7) = 7 choix (c'est idem à choisir la mauvaise réponse (C(1,7).
puis qs les puissances des probas de base

[beagle]

sinon ne fait pas l'exo, tu dis au prof que cela n'est indépendant.lorsque tu révises 70% du programme, il n' y a aucune raison que le prof tire au hasard toutes ses questions dans le sac avec des boules de ce que tu as révisé et des boules non révisées.Bref si le prof a balayé le programme une proba répétée de 0,7 cahnce de réussite n'a aucun sens.Mais bon avec quelle proba le prof validera une telle réponse?

[jocaron02]

Merci pour votre aide.
Je tente vraiment de comprendre, j'ai fais ce calcule :
raté 1 =
0,7^6 = 0.117649
0,5^5 = 0.03125
=0.00367653125
ou (donc +)
0,7^7 = 0.0823543
0,5^4 = 0.0625
=0.00514714375
raté 1 = 0.008823675


raté 0=
0,7^7 = 0.0823543
0,5^5 = 0.03125
== 0.002573571875


donc p = p raté 0 + p raté 1 =
0.008823675 + 0.002573571875
== 0.011397246875

Ce qui donnerait 1,1397% de chance de réussir, suis-je dans le bon? car ça n'a rien avoir avec ce qu'on m'a donné, ça fait 2 ou 3h que je cherche la solution à ce problème

[MJoe]

Bonjour,

Il est 18H25, j'espère qu'il n'est pas trop tard pour tenter d'expliquer le calcul de la probabilité d'avoir au moins 90% de chance de réussite au contrôle c'est-à-dire, ne faire qu'une ou zéro erreur :

J'ai fait des erreurs dans mes calculs, je recommence plus bas, désolé.
Merci @Beagle.

MJoe.

[beagle]

euh que l'on discute l'indépendance des questions de français ou de maths comme moi c'était pout causer, on oublie

mais pour faire l'exo il faut dire que indépendance succès français et succès maths
et que donc des probas indépendantes le et , le plus, l'intersection,
c'est multiplication des probas et pas addition MJoe

[MJoe]

Bonjour,

Il est 18H25, j'espère qu'il n'est pas trop tard pour tenter d'expliquer le calcul de la probabilité d'avoir au moins 90% de chance de réussite au contrôle c'est-à-dire, ne faire qu'une ou zéro erreur :

Voilà je recommence !

Je recommence les calculs !!
Probabilité de ne faire aucune erreur : P(0 erreur) :
C'est le cas où il n'y a que des succès en Français (7 succès) et en math (5 succès) :
P(0 erreur) = (0,70*0,70......*0,70) x (0,50*0,50*....0,50) = 0,7^7 x 0,5^5 = 0,002573 soit 0,2573 %

Probabilité de faire 1 erreur : P(1 erreur) :
C'est le cas où il y aura une erreur en Français (donc 6 succès en Français et 5 succès en Math) ou une erreur en Math (donc 7 succès en Français et 4 succès en Math) :
P(6 succès en Français) = 7*(0,3)*(0,70)^6 = 0,2470629
x
P(5 succès en Math) = (0,50)^5 = 0,03125
le produit donne 0,0077207 soit 0,77207 %
OU
P(7 succès en Français) = (0,70)^7 = 0,0823543
x
P(4 succès en Math) = 5*(0,50)*(0,50)^4 = 0,15625
le produit donne 0,01286 soit 1,286 %

Finalement :
P(0 erreur) + P(1 erreur) = 0,002573 + 0,0077207 + 0,01286
P(0 erreur) + P(1 erreur) = 0,02315 soit 2,32 % environ.

Il y a 2,32 % de chances d'avoir au moins 11 questions de justes (11 ou 12 questions) à ce questionnaire de Français et de Mathématiques.

MJoe.

[jocaron02]

Un grand merci, je comprends maintenant beaucoup mieux !

[MJoe]

Bonjour à tous,

Si je note X la variable aléatoire qui associe le nombre de bonnes réponses à cet examen comportant 7 réponses en Français et 5 réponses en Mathématiques, le calcul donne :

P(X = 0) = 0.000007
P(X = 1) = 0.000146
P(X = 2) = 0.001408
P(X = 3) = 0.008130
P(X = 4) = 0.031249
P(X = 5) = 0.084145
P(X = 6) = 0.162665
P(X = 7) = 0.227323
P(X = 8) = 0.227832
P(X = 9) = 0.159666
P(X = 10) = 0.074266
P(X = 11) = 0.020589 correspond à P(1 erreur)
P(X = 12) = 0.002574 correspond à P(0 erreur)

Avec bien sûr :

Voici le graphique relatif à la loi de probabilité de X :



Nota : Résultats intermédiaires :

Les probabilités d'avoir 0, 1, 2, ....., 5 bonnes réponses en Mathématiques :

Code: Tout sélectionner

 M  =
0.03125    0.15625    0.3125    0.3125    0.15625    0.03125 

Les probabilités d'avoir 0, 1, 2, ....., 7 bonnes réponses en Français :

Code: Tout sélectionner

 F  =
0.0002187    0.0035721    0.0250047    0.0972405    0.2268945    0.3176523    0.2470629    0.0823543

MJoe.

[MJoe]

Bonjour,

On peut estimer la moyenne de la promo si tous les étudiants décident de réviser à 70 % le Français et à 50 % les Mathématiques. On considère que chaque bonne réponse rapporte 5/3 points (1,6666.. points) et que les copies sont donc notées sur 20 points.
Pour un grand nombre d'étudiants, la moyenne de la promo sera proche de 12,3 sur 20 (ce qui correspond à une moyenne de 7,4 bonnes réponses sur 12).

MJoe.

[beagle]

Faut reconnaître que le prof n'est pas très malin dans son contrôle.
Il a un sac contenant 70 questions révisée par l'élève et 30 questions non révisées par l'élève pour le français.
Mouarf , le prof tire une question dans le sac, puis il tire une autre question dans le sac,
avec un peu de bol si le prof remet les questions tirées dans le sac (pour une vraie indépendance) il aura deux fois la même question!!!

On peut attendre d'un prof s'il pose 12 questions, ben que ces 12 questions balayent le programme.De telle sorte que l'indépendance prise ici pour les calculs (0,7^7 ou 0,7^6) soit sans objet.

On peut aussi penser que sur les 12 questions, c'est 3 problèmes de 4 questions qui est alors de nouveau générateur de probas liées.

Donc ne pas oublier de dire dans la rédaction du problème, nous prendrons l'hypothèse d'indépendance bien que probablement peu conforme!!!!!!!!!!!

[MJoe]

Faut reconnaître que le prof n'est pas très malin dans son contrôle.
Il a un sac contenant 70 questions révisée par l'élève et 30 questions non révisées par l'élève pour le français.
Mouarf , le prof tire une question dans le sac, puis il tire une autre question dans le sac,
avec un peu de bol si le prof remet les questions tirées dans le sac (pour une vraie indépendance) il aura deux fois la même question!!!

On peut attendre d'un prof s'il pose 12 questions, ben que ces 12 questions balayent le programme.De telle sorte que l'indépendance prise ici pour les calculs (0,7^7 ou 0,7^6) soit sans objet.

On peut aussi penser que sur les 12 questions, c'est 3 problèmes de 4 questions qui est alors de nouveau générateur de probas liées.

Donc ne pas oublier de dire dans la rédaction du problème, nous prendrons l'hypothèse d'indépendance bien que probablement peu conforme!!!!!!!!!!!

Bonjour,

Afin de remédier au problème de "2 fois la même question", moi je verrai l'énoncé comme un sujet d'examen comportant 12 questions et c'est l'étudiant qui a 70% de chance de répondre juste en Français et 50 % de chance de répondre juste en Mathématiques à chacune de ces questions.
Ainsi chaque question correspond à un "nouveau tirage".

MJoe.

[beagle]

Bonjour MJoe, j'en pense que tu formules mieux les problèmes
que celui proposé ici!

[MJoe]