Etude d'un losange

[Inexp]

Bonjour,

Voilà, je viens sur ce forum pour trouver de l'aide à un DM de mathématiques, je n'arrive pas à répondre aux questions suivantes, je n'arrive à rien et pas moyen de trouver d'aide... donc voici les questions :

1. a. Exprimer, en fonction de a, les coordonnées du point A dans le repère (O, I, J)
b. En déduire les coordonnées du point C.

2. Déterminer les coordonnées de K, de S et de B en fonction du réel a.

3. Montrer que les coordonnées de M sont (3/2 cos a ; 1/2 sin a)

4. a. Quelle est la valeur maximale de la distance OB ?
b. Quelles positions peut prendre le point B ?
c. Déterminer à quel ensemble de points appartient le point S quand le réel a varie entre 0 et 2PI

5. a. Exprimer OK en fonction de OA
b. En déduire à quel ensemble C' appartient le point K quand le réel a varie entre 0 et 2PI.

6. Soit (x;y) les coordonnées du point M
a. Calculer cos a et sin a en fonction de x et y
b. Montrer que les coordonnées de M vérifie l'équation 4/9 x² + 4y² = 1

Je joint le DM en question pour que vous ayez la figure : [URL= http://www.mediafire.com/view/9cuz8unrf77nrfa/001.jpg
]DM[/URL]

J'ai déjà réalisé la figure. J'espère avoir de l'aide. Merci

Cordialement.

[capitaine nuggets]

Salut !

Relis ton cours, toutes les formules et explications doivent-être dedans après c'est de la géométrie de 4e le losange :++:
- est un point du cercle trigonométrique (cercle de centre et de rayon ) tel qu'une mesure de est , donc ses coordonnées sont ...
- est le symétrique de par rapport à l'axe des abscisses donc ses coordonnées sont ...
- est le milieu du segment 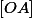donc ses coordonnées sont ...
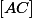- Les diagonales d'un losange se coupent en leur milieu donc est le milieu de , ainsi ses coordonnées sont ...
- est un losange donc en particulier c'est un parallélogramme et le cours de 4e nous donne alors que , et donc les coordonnées de sont ...

:+++:

[Inexp]

Déjà merci de m'aider, mais je vous préviens je suis loin d'être fort en maths :cry:

Donc par rapport à ce que vous me demandez, je dirai que les coordonnées de A sont (1a;1a) et donc les coordonnées de C sont son inverse pour l'abscisse ?

Pour K, ses coordonnées sont OA/2 et pour S je dirai donc AC/2

Par contre pour l'histoire du parallélogramme, je ne comprend pas trop :hein:

Encore merci en tout cas :++:

[capitaine nuggets]

Je voulais juste démystifié le problème en disant que la géométrie du losange avait pu être vu en 4e :we: , mais pas de soucis, c'est pour de l'aide que tu es là :++:

On t'as peut-être défini dans ton cours que dans un repère orthonormal , le cosinus et le sinus d'un angle sont respectivement l'abscisse et l'ordonnée du point du cercle de centre et de rayon vérifiant . Donc à partir de ça, quelles sont les coordonnées de en fonction de ? (N'hésite pas à faire des dessins pour y voir peut-être plus clair).

[Inexp]

Donc, Les coordonnées de A en fonction de a son (cos a; sin a) ?

[capitaine nuggets]

Donc, Les coordonnées de A en fonction de a son (cos a; sin a) ?

Oui, je te laisse essayer de répondre au 1.b) et 2. en relisant mes indications :+++:

[Inexp]

Pour la 1.b. si j'ai bien compris, ça sera A(cos -a ; sin -a )

Pour la 2. K( cos a/2 ; sin a/2) ? B( cos a*2 ; sin a*2) et par contre pour S je ne vois pas :/

[capitaine nuggets]

Pour la 1.b. si j'ai bien compris, ça sera A(cos -a ; sin -a )

Pour la 2. K( cos a/2 ; sin a/2) ? B( cos a*2 ; sin a*2) et par contre pour S je ne vois pas :/

Il y a ambiguïté dans tes écritures ... ; par exemple "cos a/2", c'est ou ? "cos a*2", c'est ou ?

Si tu as réussis à trouver les coordonnées du milieu de , tu devrais pour trouver , car est le milieu de :+++:

[Inexp]

D'accord merci.

Mais pour S je vois vraiment pas, car je ne vois pas comment faire par rapport à C.. Désolé ^^' Pourriez vous me donner quelque détails pour ce qu'il y a à faire :)

[capitaine nuggets]

D'accord merci.

Mais pour S je vois vraiment pas, car je ne vois pas comment faire par rapport à C.. Désolé ^^' Pourriez vous me donner quelque détails pour ce qu'il y a à faire

(Comme je l'ai dit, c'est la même formule que pour calculer les coordonnées du milieu K de [OA], je ne vois pas où est ta difficulté).

De manière générale, si tu as deux point M(x,y) et P(x',y'), quelles sont alors les coordonnées du milieu I de [MP] ? Il suffit donc d'appliquer cette formule pour trouver les coordonnées de S :+++: .

Et sinon, tu n'as pas répondu à mon histoire d'ambiguïté.

[Inexp]

Ah, désolé, je dirai la réponse 1 dans les 2 cas ^^

et donc pour les coordonnées de S c'est S(1/2(cos a + sin a) ; 1/2(cos -a+ sin -a) ?

[Inexp]

Je tiens à m'excuser d'avance, demain je ne serai pas disponible jusqu'à la fin probablement donc je pourrai continuer le dm demain soir, encore merci Capitaine Nuggets, j'espère que tu pourra m'aider encore un peu pour la suite, au passage, sympa le pseudo ^^
Bonne soirée

[capitaine nuggets]

Ah, désolé, je dirai la réponse 1 dans les 2 cas ^^

et donc pour les coordonnées de S c'est S(1/2(cos a + sin a) ; 1/2(cos -a+ sin -a) ?

Non, revois ton cours, la formule doit se trouver dedans, tu n'as plus qu'à l'appliquer.
Si tu as deux point M(x,y) et P(x',y'), alors les coordonnées du milieu I de [MP] sont :we:

(Tu aurais d'ailleurs pu vérifier si les coordonnées trouvées semblaient bonnes : d'après ton dessin, l'ordonnée de S est nulle. Or cos(-a)+ sin(-a) n'est pas nul en général).

[Inexp]

Ah d'accord donc j'obtiendrai S((cos a + cos-a)/2 ; (sin a + sin -a)/2) ?

Et pour la question sur l'ambiguïté, ai-je bon ?

[capitaine nuggets]

Oui, et on peut même dire mieux : et ) donc a pour coordonnées .

En ce qui concerne l'ambiguïté, tu as peux revérifier tes calculs des coordonnées du milieu de 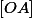avec la formule que j'ai rappelée précédemment.
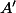Tu peux également essayer de comprendre le sens des nombres et à partir du sens de : si désigne l'abscisse du point du cercle trigonométrique tel que , alors désigne l'abscisse du point du cercle trigonométrique tel que , et désigne l'abscisse du point 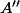du cercle de centre et de rayon 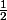tel que .

:++:

[Inexp]

Je pense comprendre, d'accord.

Par contre, j'ai regardé la suite des questions, avec vos aides je comprend mieux mais je bloque sur celle où il faut démontrer les coordonnées de M, pourriez vous m'aider ? :)

[capitaine nuggets]

Salut !

Toujours la même propriété : M est le milieu du segment [AB] donc ...

:++:

[Inexp]

Je vois comment l'obtenir, mais la justification que j'apporte me semble confuse car si je ne me trompe pas, K possède le même sinus que M ? et comme M est le symétrique de K par rapport au segment AC et que K est à (1/2)cos a, A à cos a donc M est à (3/2) cos a ?

Je comprend les mesures mais je ne sais pas si l'explication tient la route.. :(

[capitaine nuggets]

Je vois comment l'obtenir, mais la justification que j'apporte me semble confuse car si je ne me trompe pas, K possède le même sinus que M ? et comme M est le symétrique de K par rapport à la droite (AC) et que K est à (1/2)cos a, A à cos a donc M est à (3/2) cos a ?

Je comprend les mesures mais je ne sais pas si l'explication tient la route..

Oui, c'est correct, cependant, il faudrait justifier qu'effectivement M est bien le symétrique de K par rapport à (AC) et justifier que M et K ont même ordonnée.

Mais à mon avis, il est beaucoup plus simple de calculer les coordonnées de M car il est dit dans le début de l'énoncé que M est le milieu de [AB] donc les calculs sont immédiats :+++:

[Inexp]

Donc sachant que les coordonnées de B sont (cos(2a);0) et que les coordonnées de A sont (cos a; sin a) donc les coordonnées de M seront ( ( cos(2a) + cos(a) ) /2 ; ( 0 + sin(a) ) /2) ?