Etude d'un losange

[capitaine nuggets]

Donc sachant que les coordonnées de B sont (cos(2a);0) et que les coordonnées de A sont (cos a; sin a) donc les coordonnées de M seront ( ( cos(2a) + cos(a) ) /2 ; ( 0 + sin(a) ) /2) ?

Tes coordonnées de B sont fausses.

D'après une définition du cosinus d'un angle, désigne l'abscisse du point M du cercle trigonométrique tel que .

[capitaine nuggets]

En fait, B a pour coordonnées .

Je pense que tu dois confondre et . Attention, en général, :lol3:

[Inexp]

Ah d'accord donc si je reprend le calcul, les coordonnées de M seront ( ( 2cos(a) + cos(a) ) /2 ; ( 0 + sin(a) ) /2)

[capitaine nuggets]

D'où la forme des coordonnées attendue :++:

[Inexp]

D'accord, merci encore, j'ai avancé dans le DM et je ne comprend pas vraiment le sens de la question 4.c. Déterminer à quel ensemble de points appartient le point S quand le réel a varie entre 0 et 2PI

[capitaine nuggets]

D'accord, merci encore, j'ai avancé dans le DM et je ne comprend pas vraiment le sens de la question 4.c. Déterminer à quel ensemble de points appartient le point S quand le réel a varie entre 0 et 2PI

Quelle figure décrit le point lorsque varie dans dans .
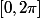
Tu l'as conjecturé dans la partie précédente, maintenant il faut le prouver :lol3:

[Inexp]

Sur Géogébra, S forme un segment quand on affiche les traces, où comme une ellipse plate (je ne sais pas si c'est le terme juste)

[capitaine nuggets]

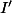
Oui, on peut même être davantage précis : paraît décrire le segment , où est le symétrique de par rapport à .

:++:

[capitaine nuggets]

Pour répondre à la question, il faut donc étudier les variations de chaque coordonnées sur [0,2\pi] (en fait, juste celle des abscisses puisque l'ordonnée est toujours nulle).

[Inexp]

Donc on peut dire que S varie entre S(-1;0) et S(1;0) ?

[capitaine nuggets]

Donc on peut dire que S varie entre S(-1;0) et S(1;0) ?

Ca n'a pas de sens de dire ca, S n'a qu'une seule paire de coordonnées.
Mais on peut dire que S décrit le segment délimité par les points de coordonnées (-1,0) et (1,0) :++:

Il faut étudier les variations de l'abscisse du point pour .

[Inexp]

Donc réaliser un tableau ?

[capitaine nuggets]

Donc réaliser un tableau ?

Normalement, c'est pas la peine, tu connais les variations de la fonction cosinus, non ?

[Inexp]

Il me semble oui, mais je ne vois absolument pas comment tourner la rédaction pour répondre à la question..

Si je dis que S décrit l'ensemble des points du segment délimité par les points de coordonnées (-1;0) et (1;0) est ce que c'est suffisant ?

[capitaine nuggets]

Il me semble oui, mais je ne vois absolument pas comment tourner la rédaction pour répondre à la question..

Si je dis que S décrit l'ensemble des points du segment délimité par les points de coordonnées (-1;0) et (1;0) est ce que c'est suffisant ?

Nam, tu paraphrases la conjecture : tu n'as rien prouvé.
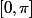
Commence par le début : quelle sont les variations de la fonction cosinus sur ? Sur ?

[Inexp]

Sur [0,\pi] la fonction cosinus varie de 1 à -1

sur [\pi,2\pi] la fonction cosinus varie de -1 à 1

[capitaine nuggets]

Sur [0,\pi] la fonction cosinus varie de 1 à -1

sur [\pi,2\pi] la fonction cosinus varie de -1 à 1

Ben voilà, à partir de ça, tu peux justifier ce que tu veux montrer :+++:

[Inexp]

Ben voilà, à partir de ça, tu peux justifier ce que tu veux montrer :+++:

Donc il faut que je tourne la phrase de réponse dans ce sens :

Comme les variations de la fonction cosinus sur [0:2pi] sont [Tableau de variation de la fonction cosinus] alors S appartient au segment délimité par les points de coordonnées (-1;0) et (1;0)

[capitaine nuggets]

Donc il faut que je tourne la phrase de réponse dans ce sens :

Comme les variations de la fonction cosinus sur [0:2pi] sont [Tableau de variation de la fonction cosinus] alors S appartient au segment délimité par les points de coordonnées (-1;0) et (1;0)

Il n'y a pas unicité d'une réponse. Part du début de ce que tu veux montrer, donne ensuite les infos qu'il faut pour obtenir le résultat voulu et ainsi conclure. :+++:

[Inexp]

Je ne comprend pas bien ce qu'il y a à faire, expliquer tout d'abord comment obtenir S, dire pourquoi son sinus sera toujours nul, expliquer la variation du cosinus puis conclure que l'ensemble des points de S appartiennent au segment de coordonnées (-1;0) et (1;0) ?