Etude de fonction

[nico033]

Bonjour, jai une etude de fonction a faire pour mardi et j'aimerai que lon mexplique certaines questions que je nai pas bien compris
pourriez me corriger sil vous plait

voici le sujet, les deux parties ne sont pas indépendantes

partie A

soit g la fonction definie sur IR Par g(x) = 4-x-exp(x).

1. limites de g en -infini et en + infini j'ai reussi

2. variation de g et tableau (jai reussi).

3. demontrer que l'équation g(x) = 0 admet une unique solution alpha sur IR telle que alpha appartient [1,073; 1,074] (je pense avoir reussi jai calcule g(1,073) et g(1,074) ils sont de signes contraires donc il existe bien un reel alpha solution de cette équation (theoreme des valeurs intermediaires) est ce cela?

4. en deduire le signe de g(x) sur IR ( jai un doute, j'ai trouvé que g'(x) = -exp(x)-1 jai trouvé que la variation de g(x) etait negative sur IR.
donc je penserai que le signe de g(x) est négatif? est ce cela?

partie B
5. soit la fonction f definie sur IR par f(x) = (3-x)(1-exp(-x)).
etude du signe de f(x), j'ai trouvé que f'(x) = -(exp(x)+x-4)*exp(-x).
mais pour etudier le signe de f(x) je ne sais pas trop, je sais que exp(x) est toujours positive pour tout x, donc f'(x) aurai le signe de -(exp(x)+x-4)? mais le probleme cest que jai encore une exponentielle ? donc comment faire sil vous plait.

6. limites de f en - infini et + infini (jai reussi).

et pour cette question je sais pas du tout:
montrer que
intégrale exp(x)*f'(x) dx = (-alpha²+10alpha-6)/(2) (entre alpha et 0).

[fonfon]

salut,

4. en deduire le signe de g(x) sur IR ( jai un doute, j'ai trouvé que g'(x) = -exp(x)-1 jai trouvé que la variation de g(x) etait negative sur IR.
donc je penserai que le signe de g(x) est négatif? est ce cela?

on te demande en deduire donc il faut dejà te servir de la question precedente

tu sais que ta fonction est strictement decroissante et qu'elle s'annule pour ds [1.073;1.074] donc sur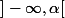 g(x) est positive et sur g(x) est negative

partie B
5. soit la fonction f definie sur IR par f(x) = (3-x)(1-exp(-x)).
etude du signe de f(x), j'ai trouvé que f'(x) = -(exp(x)+x-4)*exp(-x).
mais pour etudier le signe de f(x) je ne sais pas trop, je sais que exp(x) est toujours positive pour tout x, donc f'(x) aurai le signe de -(exp(x)+x-4)? mais le probleme cest que jai encore une exponentielle ? donc comment faire sil vous plait.

ok pour la dérivée en ecrivant que f'(x)=g(x)*e^(-x) c'est pas mieux, tu sais que e^(-x)>0 donc f'(x) est du signe de g(x) or tu connais le signe de g(x) donc celui de f'(x) et donc les variations de f et enfin son signe