novicemaths a écrit:Bonsoir
=\frac{x^2-x-5}{x-3})
Domaine de définition

Donc

Pour les limites:
On a
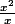
donc on fera la limite sur x.

et

=9-3-5=1)
 = 0^+)
=0^-)
On demande démontrer que tout
=x+2+\frac{1}{x-3})
Pour tout
=x+2+\frac{1}{x-3}=\frac{(x+2)(x-3)+1}{x-3}=\frac{x^2-3x+2x-6+1}{x-3}=\frac{x^2-x-5}{x-3})
Je ne vois pas comment démontrer un asymptote oblique.
On calcule toujours les limites aux bornes du domaine de définition : il faut donc calculer quatre limites : une en

, une en

, une en

pour valeurs inférieures et enfin une en

par valeur supérieures.
Puisque

est une valeur interdite :

n'est pas continue en

, donc
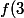)
n'existe pas et encore moins la limite de

en

.
La question te demandant de trouver une autre forme pour
)
que celle donnée au début, est destinée à te donner une équation de cette asymptote oblique : il s'agit de la droite d'équation
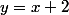
.
Si tu n'as aucune idée, tu peux toujours chercher son équation : la droite d'équation

est asymptote oblique à la courbe de

si et seulement si la limite en

et

de
-(ax+b))
est nulle :+++:
Pour la deuxième fonction, on ne te donne pas l'expression de
)
faisant apparaître une équation de droite de l'asymptote (si elle existe). Détermine donc trois réels

tels que

.
)
peut s'écrire sous une telle forme parce que la différence du degré du numérateur par le degré du dénominateur vaut

(le degré du terme
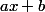
) et que le dénominateur est une fonction affine en

(cela fait apparaître le

).
Pour la troisième fonction, tes limites en l'infini se calculent en exprimant

sous forme de quotient de deux fonctions :+++:
