Est ce qu'on peut avoir un trapèze non droit ayant les diagonales perpendiculaires

par **mohamedalichelly** » 12 Juin 2015, 16:34

Bonjour
est ce qu'on peut avoir un trapèze non droit ayant les diagonales perpendiculaires ?

par **mohamedalichelly** » 12 Juin 2015, 16:38

Bonjour
si les diagonales d'un quadrilatère sont perpendiculaires alors il s'agit d'un losange ou carré n'est ce pas ?

par **zygomatique** » 12 Juin 2015, 16:48

salut

oui !!!

il suffit de prendre un carré ABCD

alors toute parallèle à (AB) coupe les deux diagonales en deux points I et J et ABIJ est un trapèze .... isocèle ....

par **chombier** » 12 Juin 2015, 16:50

mohamedalichelly a écrit:Bonjour
si les diagonales d'un quadrilatère sont perpendiculaires alors il s'agit d'un losange ou carré n'est ce pas ?

Pas forcément. Si un les diagonales d'un parallélogramme sont perpendiculaires alors ce parallélogramme est un losange

Exemple de quadrilatère dont les diagonales sont perpendiculaires mais qui n'est pas un losange (et encore moins un carré) :

par **chombier** » 12 Juin 2015, 16:56

zygomatique a écrit:salut

oui !!!

il suffit de prendre un carré ABCD

alors toute parallèle à (AB) coupe les deux diagonales en deux points I et J et ABIJ est un trapèze .... isocèle ....

Ses diagonales sont-elles perpendiculaires ? Je n'en suis pas sur du tout...

par **chombier** » 12 Juin 2015, 16:59

mohamedalichelly a écrit:Bonjour
est ce qu'on peut avoir un trapèze non droit ayant les diagonales perpendiculaires ?

En voici un :

Tu peux remarquer que n'importe quel losange qui n'est pas un carré réponds aux contraintes que tu as fixées :
- c'est un losange, donc c'est un trapèze
- ce n'est pas un carré, donc c'est un trapèze non droit
- c'est un losange, donc ses diagonales sont perpendiculaires

par **mathafou** » 12 Juin 2015, 17:11

Bonjour

pour "fabriquer" un trapèze à diagonales perpendiculaires, c'est facile :

on trace deux droites perpendiculaires quelconques

et

et deux droites parallèles

et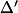

quelconques et le tour est joué

il est donc facile d'obtenir une infinité de tels trapèzes
la question est généralement d'obtenir un tel trapèze ayant en plus d'autres propriétés ...

par **mohamedalichelly** » 12 Juin 2015, 17:15

zygomatique a écrit:salut

oui !!!

il suffit de prendre un carré ABCD

alors toute parallèle à (AB) coupe les deux diagonales en deux points I et J et ABIJ est un trapèze .... isocèle ....

les diagonales [BJ] et [AI] sont perpendiculaires ?????
c'est ça ma question.

par **mohamedalichelly** » 12 Juin 2015, 17:17

chombier a écrit:En voici un :

Tu peux remarquer que n'importe quel losange qui n'est pas un carré réponds aux contraintes que tu as fixées :
- c'est un losange, donc c'est un trapèze
- ce n'est pas un carré, donc c'est un trapèze non droit
- c'est un losange, donc ses diagonales sont perpendiculaires

pour le premier schéma comment montrer que les diagonales sont perpendiculaires

par **nodjim** » 12 Juin 2015, 17:51

Tu peux très bien avoir un trapèze non droit avec des diagonales perpendiculaires. Tu traces d'abord ta petite base, tu fais partir des extrémités 2 diagonales perpendiculaires. Au dela de leur intersection, tu peux tracer la grande base de la longueur que tu veux. Elle n'aura pas en général la longueur de la petite base.

par **mohamedalichelly** » 12 Juin 2015, 17:57

Soit un triangle ABC telque AB=2 racine de 5 ; AC= 5; BC=3
Soient I et J les milieux respectives de [AB] et [AC].
Montrer que [CI] et [BJ] sont perpendiculaires ???

par **chombier** » 12 Juin 2015, 17:58

mohamedalichelly a écrit:Soit un triangle ABC telque AB=2 racine de 5 ; AC= 5; BC=3
Soient I et J les milieux respectives de [AB] et [AC].
Montrer que [CI] et [BJ] sont perpendiculaires ???

Tu ne pouvait pas des le départ nous donner l'énoncé de ton exercice au lieu de tourner autour du pot ?

Je veux dire, c'est super bien que tu aies des questions et des pistes de résolution, mais c'est encore mieux si on voit où tu veux en venir :lol3:

par **mathafou** » 12 Juin 2015, 18:09

Ah !! en fait la question est sur les triangles avec deux médianes perpendiculaires ...

une piste : les médianes se coupent en G
utiliser le théorème de la médiane pour exprimer les longueurs de CI et BJ, donc GC et GB
puis Pythagore sur GBC

sans le théorème de la médiane ... cela revient à le démontrer.

par **zygomatique** » 12 Juin 2015, 19:42

chombier a écrit:Ses diagonales sont-elles perpendiculaires ? Je n'en suis pas sur du tout...

bon alors précisons !!!

soit ABCD un carré de centre O

et une droite parallèle à [AB] coupant les diagonales entre O et C et O et D ....

donc tels que [BJ] et [AI] soient les diagonales ....

I dans [OC] et J dans [OD] ....

par **mathafou** » 12 Juin 2015, 19:59

zygomatique a écrit:bon alors précisons !!!

soit ABCD un carré de centre O

et une droite parallèle à [AB] coupant les diagonales entre O et C et O et D ....

donc tels que [BJ] et [AI] soient les diagonales ....

I dans [OC] et J dans [OD] ....

ton cas particulier est intéressant mais donne un trapèze qui est en plus isocèle et pas "le cas général"
de toute façon une figure illustrant correctement le propos aurait été bien venue
tu pourrais aussi bien partir d'un losange au lieu d'un carré, voire même pas de carré ni de losange du tout mais juste ses "diagonales" et rien d'autre ... (deux droites perpendiculaire et une sécante commune AB, les points C et D ne servent à rien)

mais de toute façon, vu que le problème n'a aucun rapport avec des diagonales perpendiculaires dans un trapèze mais avec des médianes perpendiculaires dans un triangle ... la discussion ici est inutile est sans rapport avec la vraie question
(et vu les multipost de mohamedalichelly)

par **zygomatique** » 12 Juin 2015, 20:08

mathafou a écrit:ton cas particulier est intéressant mais donne un trapèze qui est en plus isocèle et pas "le cas général"
de toute façon une figure illustrant correctement le propos aurait été bien venue
tu pourrais aussi bien partir d'un losange au lieu d'un carré, voire même pas de carré ni de losange du tout mais juste ses "diagonales" et rien d'autre ... (deux droites perpendiculaire et une sécante commune AB, les points C et D ne servent à rien)

mais de toute façon, vu que le problème n'a aucun rapport avec des diagonales perpendiculaires dans un trapèze mais avec des médianes perpendiculaires dans un triangle ... la discussion ici est inutile est sans rapport avec la vraie question
(et vu les multipost de mohamedalichelly)

je ne comprends pas ....

proposer toute sorte de quadrilatère ayant des diagonales perpendiculaires ne répond pas à la première question posée ...

mon premier post y répond avec quelques imprécisions (certes !!)

un trapèze ayant des diagonales perpendiculaires ... et que je précise isocèle dans mon premier post ...

chombier a cherché la petite bête (a raison) et propose un cas plus général ...ok

:lol3:

par **mathafou** » 12 Juin 2015, 20:22

zygomatique a écrit:je ne comprends pas ....

proposer toute sorte de quadrilatère ayant des diagonales perpendiculaires ne répond pas à la première question posée ...

mon premier post y répond avec quelques imprécisions (certes !!)

un trapèze ayant des diagonales perpendiculaires ... et que je précise isocèle dans mon premier post ...

chombier a cherché la petite bête (a raison) et propose un cas plus général ...ok

:lol3:

les réponses apportées à la question initiale de ce topic certes

mais fondamentalement le demandeur ne voulait pas du tout poser cette question mais celle là :

mohamedalichelly a écrit:Soit un triangle ABC telque AB=2 racine de 5 ; AC= 5; BC=3
Soient I et J les milieux respectives de [AB] et [AC].
Montrer que [CI] et [BJ] sont perpendiculaires ???

qu'il a fini par avouer suite à la question "mais quel est ton véritable énoncé ?"
et il avait posé la présente question sur les trapèzes suite à une réinterprétation fautive de son propre énoncé, au lieu de le donner tel quel, ce qui fait perdre un peu son temps à tout le monde ici.

ce topic ci est effectivement intéressant mais sans rapport avec la vraie question du demandeur. (la question qu'il a fini par avouer sur les triangles)

Est ce qu'on peut avoir un trapèze non droit ayant les diagonales perpendiculaires

est ce qu'on peut avoir un trapèze non droit ayant les diagonales perpendiculaires

Qui est en ligne