Comment démontrer que les diagonales d'un quadrilatère ont u

[Teamis]

[FONT=Comic Sans MS]Bonjours!
j'ai fais la première partie de l'exercice ( le a) ) mais je ne comprends pas comment ont peux démontrer que les diagonales d'un quadrilatère à un même milieu :triste:

Je vous donne l'énoncer ( au cas où vous le voulez )

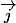
Le plan étant muni d'un repère ( O, , ), soient A ( -2 ; 3 ) , B ( 6 ; 4 ) , C ( 5 ; -1 ) et D ( -4 ; -2 )

a) Grahique ( Je l'ai fais )
b) Démontrer que les diagonales du quadrilatère ABCD ont même milieu.
Que peut-on en déduire ?

Je n'arrive pas à faire la b).. :help:



Merci d'avance de votre lecture et aux personnes m'aideront. :lol3:[/FONT]

[SaintAmand]

Bonsoir,

b) Démontrer que les diagonales du quadrilatère ABCD ont même milieu.

S'il te viens à l'idée d'ouvrir ton cours ou ton manuel, tu y verras une formule qui donne les coordonnées du milieu d'un segment à partir des coordonnées de ses extrémités.

Que peut-on en déduire ?

Cours de quatrième sur les quadrilatères.

[Teamis]

Bonsoir,

S'il te viens à l'idée d'ouvrir ton cours ou ton manuel, tu y verras une formule qui donne les coordonnées du milieu d'un segment à partir des coordonnées de ses extrémités.

Dans mon cours, il y'a une formule mais c'est pour la distance c'est celle ci : AB² = p² + p²
Sinon, il y'en a pas d'autre... :/

Cours de quatrième sur les quadrilatères.

J'ai des lacunes pour les connaissance de 4ème, mon prof n'était pas super..

[SaintAmand]

Dans mon cours, il y'a une formule mais c'est pour la distance c'est celle ci : AB² = p² + p²

Elle est bizarre ta formule. Bref, tu es en seconde n'est-ce pas ? Donc dans ton manuel il y a une formule qui donne les coordonnées du milieu d'un segment.

J'ai des lacunes pour les connaissance de 4ème, mon prof n'était pas super..

Oh l'excuse... garde-la pour tes parents

[Teamis]

Oh l'excuse... garde là pour tes parents

Non, c'est vrai ! c'étais même pas un véritable prof, je crois que c'étais un monsieur qui voulais faire un travail où il y'avais beaucoup de mathematique (ex : architecte ect...) donc il ne savait pas expliquer..

[Teamis]

Elle est bizarre ta formule. Bref, tu es en seconde n'est-ce pas ? Donc dans ton manuel il y a une formule qui donne les coordonnées du milieu d'un segment.


Oh l'excuse... garde-la pour tes parents

J'ai chercher dans tout le livre et j'ai pas trouver ! :doh:

[SaintAmand]

J'ai chercher dans tout le livre et j'ai pas trouver ! :doh:

Je suppose que tu sais exprimer les coordonnées d'un vecteur à partir des coordonnées des extrémités d'un représentant:

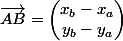
Donc soit A et B deux points du plan muni d'un repère. Soit I le milieu du segment [AB].

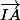
1. Quelle relation y a-il entre les vecteurs et ?
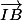
2. En déduire les coordonnées de I en fonction de celles de A et B.

[Teamis]

Je suppose que tu sais exprimer les coordonnées d'un vecteur à partir des coordonnées des extrémités d'un représentant:

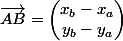
Donc soit A et B deux points du plan muni d'un repère. Soit I le milieu du segment [AB].

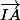
1. Quelle relation y a-il entre les vecteurs et ?
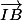
2. En déduire les coordonnées de I en fonction de celles de A et B.

1.L'abscisse du point I est égale à la demi-somme des abscisse A et B
L'ordonnée du point I est égale à la demi-somme des abscisse A et B

2. Avec les coordonnées précédentes de A et B, on obtient : I ( -8 - 3/4 )

[SaintAmand]

1.L'abscisse du point I est égale à la demi-somme des abscisse A et B
L'ordonnée du point I est égale à la demi-somme des abscisse A et B

Finalement tu as trouvé la page.

2. Avec les coordonnées précédentes de A et B, on obtient : I ( -8 - 3/4 )

Es-tu certaine que la demi somme de 6 et de -2 soit -8 ? De même la demi-somme de 4 et de 3 n'est certainement pas -3/4.

T'as raison, ton prof de collège était vraiment nul ^_^

[sad13]

les diagonales du quadrilatère ABCD ont même milieu donc....