1 ereS DM trinome
18 messages
- Page 1 sur 1
1 ereS DM trinome
bonjour, j'ai un Dm de math à rendre mais je suis bloquée à une question et pas moyen d'en trouver la solution. je vous donne l'énoncé
Déterminer les valeurs du réel m tels que : -x²+mx - 4m+1 inferieur ou egal à 0 pour tout réel x.
j'espère que vous pourrez m'aider à résoudre ceci en vous remerciant ;)
MissLady
Déterminer les valeurs du réel m tels que : -x²+mx - 4m+1 inferieur ou egal à 0 pour tout réel x.
j'espère que vous pourrez m'aider à résoudre ceci en vous remerciant ;)
MissLady
mamanprof a écrit:Calcule le discriminant (en fonction de m).
Que doit vérifier ce discriminant pour que ton polynôme ne s'annule jamais ? (condition suffisante pour qu'il soit toujours négatif, puisque le coefficient devant x² l'est).
Cela devrait répondre à ta question.
je n'ai pas compris votre réponse... l'inéquation doit etre < ou =
et comment calculer le discriminant, puisqu'il ne s'agit pas d'un trinôme ax²+bx+c
Tu as une expression de la forme ax² + bx + c, même si les coefficients dépendent de m :
a = -1
b =
c = -4m + 1
Si le discriminant est négatif, il n'y aura pas de solution et le trinôme sera toujours négatif (car a=-1 < 0)
Si le discriminant est nul, il y aura une solution, c'est le cas où le trinôme vaut 0.
Tu dois donc trouver les valeurs de m qui rendront le discriminant négatif ou nul.
a = -1
b =
c = -4m + 1
Si le discriminant est négatif, il n'y aura pas de solution et le trinôme sera toujours négatif (car a=-1 < 0)
Si le discriminant est nul, il y aura une solution, c'est le cas où le trinôme vaut 0.
Tu dois donc trouver les valeurs de m qui rendront le discriminant négatif ou nul.
mamanprof a écrit:Tu as une expression de la forme ax² + bx + c, même si les coefficients dépendent de m :
a = -1
b =
c = -4m + 1
Si le discriminant est négatif, il n'y aura pas de solution et le trinôme sera toujours négatif (car a=-1 < 0)
Si le discriminant est nul, il y aura une solution, c'est le cas où le trinôme vaut 0.
Tu dois donc trouver les valeurs de m qui rendront le discriminant négatif ou nul.
Et le mx, il se trouve ou dans a,b ou c ?
MissLady a écrit:bonjour, j'ai un Dm de math à rendre mais je suis bloquée à une question et pas moyen d'en trouver la solution. je vous donne l'énoncé
Déterminer les valeurs du réel m tels que : -x²+mx - 4m+1 inferieur ou egal à 0 pour tout réel x.
j'espère que vous pourrez m'aider à résoudre ceci en vous remerciant
MissLady
Les coefficients du trinome sont: (-1,m,-4m+1)
avec ça, on peut calculer le
qui aura lui-même un
mathelot a écrit:Les coefficients du trinome sont: (-1,m,4m+1)
avec ça, on peut calculer le
qui aura lui-même un
du coup,le
merci ^^
MissLady a écrit:up s'il vous plait
si on fait le delta de -x² +mx-4m+1, on obtient m²+16m+4 qui est une fonction trinome. Donc, le delta que je vais calculer, si il existe des racines, sera solution de mon inéquation de départ ou il yt a des étape à faire ensuite ? merci
on calcule son discriminant
ou
MissLady a écrit:a pas compris ton explication, les resultat du tableau de signe de m²-16m+4, serait les resultat popur mon inéquation x²+mx-4m+1 ?
j'ai calculé les racines de m²-16m+4, cela donne 8-2racine de 15 et 8-2 racine de 15, a quoi correspondent ces résultats ?
merci d'avance
alors si
admet deux racines.
Quelques précisions:
Il ne faut pas confondre les deux polynômes du second degré:
Le premier est celui dont la variable est x: x²+mx-4m+1 et le second dont la variable est m :m²-16m+4
Pour étudier le signe de ce polynôme il faut calculer et en fonction du signe de ce discriminant, on peut faire le tableau de signe de x²+mx-4m+1
et en fonction du signe de ce discriminant, on peut faire le tableau de signe de x²+mx-4m+1
Pour que x²+mx-4m+1 soit de signe constant, il ne faut pas qu'il y ait deux racines distinctes donc que soit négatif ou nul.
soit négatif ou nul.
Il faut donc que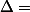 m²-16m+4 soit donc négatif ou nul.
m²-16m+4 soit donc négatif ou nul.
Tu dois donc étudier le signe de m²-16m+4 dont la variable est m (c'est ce m que tu cherches maintenant).
Il faut donc calculer le discriminant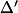 (a=1, b=-16 et c=4) et faire le tableau de signes du polynôme (de variable m) m²-16m+4
(a=1, b=-16 et c=4) et faire le tableau de signes du polynôme (de variable m) m²-16m+4
En espérant que cela te permette de comprendre la démarche suivie depuis le début...
J-F Lecarpentier
Il ne faut pas confondre les deux polynômes du second degré:
Le premier est celui dont la variable est x: x²+mx-4m+1 et le second dont la variable est m :m²-16m+4
Pour étudier le signe de ce polynôme il faut calculer
Pour que x²+mx-4m+1 soit de signe constant, il ne faut pas qu'il y ait deux racines distinctes donc que
Il faut donc que
Tu dois donc étudier le signe de m²-16m+4 dont la variable est m (c'est ce m que tu cherches maintenant).
Il faut donc calculer le discriminant
En espérant que cela te permette de comprendre la démarche suivie depuis le début...
J-F Lecarpentier
mathelot a écrit:alors si, le trinome en x
admet deux racines.
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
