équations du second degrée help

[laetidom]

Merci pour ton aide elle est grandement appréciée.

Comment tu fais les symboles de math sur le clavier de l'ordinateur je ne l'ai trouve pas.

Merci cidou également pour ton assiduité, c'est très agréable ! Bonne nuit !

les symboles de math : lycee/ecrire-des-belles-formules-mathematiques-balises-tex-t70548.html

[cidou]

Bonsoir

Comment développé vous l'équation suivante:

(-x+7) (5x+3)-(x+5) ( x-5)

je ne m'en sors pas au niveau des signes surtout dans la deuxième partie.

[laetidom]

Bonsoir

Comment développé vous l'équation suivante:

(-x+7) (5x+3)-(x+5) ( x-5)

je ne m'en sors pas au niveau des signes surtout dans la deuxième partie.

Bonsoir,

Tout simplement :
(-x+7)(5x+3) - (x+5)( x-5) :

(-x+7)(5x+3) = -5x² -3x +35x +21

(x+5)( x-5) = "a² - b²" = x² - 5² = x² - 25

donc (-x+7)(5x+3) - (x+5)( x-5) = -5x² -3x +35x +21 - (x² - 25) = -5x² -3x +35x +21 - x² + 25 ===> à réduire . . .

[cidou]

Ok j'avais du mal à développer :
(x+5)( x-5)
sans utiliser l'identité remarquable

je trouvais - (x²-5x +5x -25)

donc – x²+25

ce qui reviens au même,je m'embrouillais avec le – devant la parenthèse qui change tous les signes.

Pour l'identité remarquable je croyais que c'était

(a-b) (a+b) = a²-b²

et non l'inverse, mais comme la multiplication est commutative ça marche dans les deux sens c'est ça ?

[laetidom]

Ok j'avais du mal à développer :
(x+5)( x-5)
sans utiliser l'identité remarquable

je trouvais - (x²-5x +5x -25)

donc – x²+25 Oui !

ce qui reviens au même, je m'embrouillais avec le – devant la parenthèse qui change tous les signes.

Pour l'identité remarquable je croyais que c'était

(a-b) (a+b) = a²-b²

et non l'inverse, mais comme la multiplication est commutative ça marche dans les deux sens c'est ça Oui, ça marche dans les 2 sens !?

[laetidom]

donc le résultat final donne . . . ?

[cidou]

-6x²+32x+46

[laetidom]

-6x²+32x+46

Ca me convient également ! Bonne soirée.

[cidou]

merci pour ton aide a+

[laetidom]

merci pour ton aide a+

Je t'en prie, content d'avoir été utile, @+ sur le forum.

[cidou]

Bonsoir

Une petite question pour demain.

On à
(2x-1)²
la réponse est

4x²-4x+1

pourquoi ne peut on appliqué
la règle de l'idientite remarquable

a²-b²
4x²-1²
si on develloppe

(4x²-1)(4x²+1)

mais le résultat est faux

16x+4x²-4x²-1

[Lostounet]

Bonsoir,

C'est faux car tout simplement n'est pas

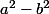
Essaye avec deux nombres a et b (pas tous les deux nuls) et tu verras.

[cidou]

Exact par contre on peut utiliser l'identité remarquable (a-b)² pour développer.

[Lostounet]

Oui !
Dans ce cas:
(2x-1)² est de la forme (a - b)^2 avec a = 2x et b = 1
donc (2x - 1)^2 = (2x)^2 - 2*(2x)*1 + 1 = 4x^2 - 4x + 1

[cidou]

Dans les exercice que je fais il est noté que

(1-2x) est egal à -(2x-1) donc -2x+1 si je ne me trompe pas
hors je ne comprend pas puisse qu il est dis que la soustraction n est pas commutative?

[cidou]

Oui !
Dans ce cas:
(2x-1)² est de la forme (a - b)^2 avec a = 2x et b = 1
donc (2x - 1)^2 = (2x)^2 - 2*(2x)*1 + 1 = 4x^2 - 4x + 1

pourquoi b n est pas égal a -1 comme dans la formule (a-b)²

[Lostounet]

Oui, la soustraction est non commutative. Cela signifie que a - b est différent de b - a en général.
[Contrairement par exemple à la multiplication qui elle est commutative: a*b = b*a pour tous nombres a et b]

Mais attention, ici la propriété en jeu n'est pas la commutativité de la soustraction ...
Pour mieux comprendre cette propriété, si tu as 20 euros, et que je te dis:
donne moi 4 euros puis 3 euros, tu auras 20 - 4 - 3 = 13 euros

c'est vraiment pareil que si je t'avais dit: donne moi 7 euros directement
20 - 4 - 3 = 20 - (4 + 3) = 20 - 7 tu vois?

donc enlever (2x - 1), c'est faire - (2x - 1), je peux d'abord enlever (2x) puis enlever (-1)
-2x - (-1) = -2x + 1

[Lostounet]

pourquoi b n est pas égal a -1 comme dans la formule (a-b)²

Parce que, si b valait - 1, et que a = 2x,
alors (a - b) serait a - b = (2x) - (-1) = 2x + 1 c'est pas l'expression demandée..

[Lostounet]

(a-b) (a+b) = a²-b²

et non l'inverse, mais comme la multiplication est commutative ça marche dans les deux sens c'est ça ?

Ceci n'a pas de sens !
Cela marche dans les deux sens grace au signe "=" !
X = Y équivaut à Y = X
La commutativité de la multiplication n'intervient pas du tout. A la limite, tu peux dire que
(a - b) * (a + b) = (a + b)*(a - b) = a^2 - b^2 et là OK sinon revois la définition

[cidou]

Oui, la soustraction est non commutative. Cela signifie que a - b est différent de b - a en général.
[Contrairement par exemple à la multiplication qui elle est commutative: a*b = b*a pour tous nombres a et b]

Mais attention, ici la propriété en jeu n'est pas la commutativité de la soustraction ...
Pour mieux comprendre cette propriété, si tu as 20 euros, et que je te dis:
donne moi 4 euros puis 3 euros, tu auras 20 - 4 - 3 = 13 euros

c'est vraiment pareil que si je t'avais dit: donne moi 7 euros directement
20 - 4 - 3 = 20 - (4 + 3) = 20 - 7 tu vois?

donc enlever (2x - 1), c'est faire - (2x - 1), je peux d'abord enlever (2x) puis enlever (-1)

-2x - (-1) = -2x + 1

Oui je comprend mieux maintenant

Merci.