équations du second degrée help
89 messages
- Page 4 sur 5 - 1, 2, 3, 4, 5
Re: équations du second degrée help
Bonjour Cidou,
Et si tu multipliais les deux côtés par 2?
Et si tu multipliais les deux côtés par 2?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: équations du second degrée help
dans le corrigé ces ecrit
x+1+6=2+3x+5
Tu peux développer l'opération stp
x+1+6=2+3x+5
Tu peux développer l'opération stp
Modifié en dernier par cidou le 15 Mai 2016, 19:27, modifié 1 fois.
Re: équations du second degrée help
(2x-6)2x=0
les réponse sont x= 0 ou x=3
comment trouver 3 je ne comprend pas ?
Peux tu développer stp.
les réponse sont x= 0 ou x=3
comment trouver 3 je ne comprend pas ?
Peux tu développer stp.
Re: équations du second degrée help
Si je te dis TRUC fois BIDULE = 0 ... Tu vas me dire ... tu es bien malin Lostounet mais je devine que soit TRUC = 0 soit BIDULE = 0 !!!
Ici c'est pareil (2x - 6)*(2x) = 0 ... c'est soit (2x - 6) qui vaut 0 soit 2x qui vaut 0
2x - 6 = 0 <=> 2x = 6 <=> x = 3
ou bien 2x = 0 <=> x = 0
Ici c'est pareil (2x - 6)*(2x) = 0 ... c'est soit (2x - 6) qui vaut 0 soit 2x qui vaut 0
2x - 6 = 0 <=> 2x = 6 <=> x = 3
ou bien 2x = 0 <=> x = 0
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: équations du second degrée help
Peut on développer l'équation suivante.
4-(x+1)²=0
avec l'identité remarquable a²-b²
je n'arrive pas au même résultat avec la forme x²=a
Merci.
4-(x+1)²=0
avec l'identité remarquable a²-b²
je n'arrive pas au même résultat avec la forme x²=a
Merci.
Re: équations du second degrée help
Hey Cidou,
Crois-moi, pour progresser il faut vraiment que tu essayes de faire un raisonnement d'écrire
Tu n'apprendras qu'en faisant des erreurs..
Crois-moi, pour progresser il faut vraiment que tu essayes de faire un raisonnement d'écrire
Tu n'apprendras qu'en faisant des erreurs..
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: équations du second degrée help
Lostounet a écrit:Hey Cidou,
Crois-moi, pour progresser il faut vraiment que tu essayes de faire un raisonnement d'écrire
Tu n'apprendras qu'en faisant des erreurs..
ok merci pour le conseil.
Re: équations du second degrée help
Et donc, comment résoudre:
4-(x+1)²=0 ?
4-(x+1)²=0 ?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: équations du second degrée help
comme ca je crois je m'etais trompé dans les sisignes
2²-(x+1)=0
(2-(x+1)) (2+(x+1))=0
(2-x-1)(2+x+1)=0
(-x+1)(x+3)=0
donc -x=-1 x=1
et x = -3
2²-(x+1)=0
(2-(x+1)) (2+(x+1))=0
(2-x-1)(2+x+1)=0
(-x+1)(x+3)=0
donc -x=-1 x=1
et x = -3
Re: équations du second degrée help
C'est ça, très bien!
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: équations du second degrée help
Bonsoir.
Quelqu'un peut m'aider a factoriser en utilisant les identitées remarquable l'équation suivante je ne m'en sors pas a cause des signes moins.
-x²+2x+3=4
Merci
Quelqu'un peut m'aider a factoriser en utilisant les identitées remarquable l'équation suivante je ne m'en sors pas a cause des signes moins.
-x²+2x+3=4
Merci
Re: équations du second degrée help
Salut !
Réécris ton équation sous la forme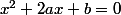 , où
, où  et
et  sont deux réels que tu préciseras.
sont deux réels que tu préciseras.
Ensuite, remarque que puisque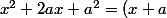^2) , on a
, on a 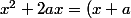^2-a^2) . Ainsi, résoudre
. Ainsi, résoudre 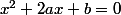 revient à résoudre
revient à résoudre ^2-a^2+b =0) .
.

Réécris ton équation sous la forme
Ensuite, remarque que puisque
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: équations du second degrée help
capitaine nuggets a écrit:Salut !
Réécris ton équation sous la forme, où
et
sont deux réels que tu préciseras.
Ensuite, remarque que puisque, on a
. Ainsi, résoudre
revient à résoudre
.
Salut merci de ta réponse mais il n'y a pas plus simple
dans le bouquin il arrive au résultat -(x-1)²=0
J'aimerai comprendre comment arriver a ce résultat mois je trouve
-x²+2x+3=4
-x²+2x-1=0
x²+2x+1²=0
donc on factorise avec (a+b)²
(x+1)²=0
x=-1
hors la réponse est 1
il trouve -(x-1)²=0
je m'embrouille avec les – quand on doit remplacer par le nombre b et qu il est negatif je ne sais pas si il faut juste mettre b ou -b!
Re: équations du second degrée help
cidou a écrit:
J'aimerai comprendre comment arriver a ce résultat mois je trouve
-x²+2x+3=4
-x²+2x-1=0
x²+2x+1²=0 erreur ici
Comment tu passes de -x^2 + 2x - 1 = 0 à la ligne suivante? tu multiplies par (-1) les deux membres de l'équation et cela te donne:
(-1)*[-x^2 + 2x - 1] = (-1)*0
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: équations du second degrée help
Lostounet a écrit:cidou a écrit:
J'aimerai comprendre comment arriver a ce résultat mois je trouve
-x²+2x+3=4
-x²+2x-1=0
x²+2x+1²=0 erreur ici
Comment tu passes de -x^2 + 2x - 1 = 0 à la ligne suivante? tu multiplies par (-1) les deux membres de l'équation et cela te donne:
(-1)*[-x^2 + 2x - 1] = (-1)*0Et ça c'est pas de la forme
mais
Ok je ne connais pas cette façon de simplifier!
Tu peux me l'expliquer
Re: équations du second degrée help
Tu ne sais pas que, dans une équation, on peut multiplier et diviser les deux cotés par un même nombre?
Et tu ne connais pas la règle de distributivité suivante ? Si au supermarket j'achète deux sachets, avec dans chaque sachet 1 pomme et une poire, alors en tout j'ai:
DEUX(Pomme + Poire) c'est DEUX POMMES + DEUX POIRES
Ben ici c'est pareil, pour tous nombres k, a et b on a k(a + b) = k*a + k*b
Je distribue le (-1):
(-1) *(-x^2 + 2x - 1) = (-1)*(-x^2) + (-1)*(2x) + (-1)*(-1) = x^2 - 2x + 1
Et tu ne connais pas la règle de distributivité suivante ? Si au supermarket j'achète deux sachets, avec dans chaque sachet 1 pomme et une poire, alors en tout j'ai:
DEUX(Pomme + Poire) c'est DEUX POMMES + DEUX POIRES
Ben ici c'est pareil, pour tous nombres k, a et b on a k(a + b) = k*a + k*b
Je distribue le (-1):
(-1) *(-x^2 + 2x - 1) = (-1)*(-x^2) + (-1)*(2x) + (-1)*(-1) = x^2 - 2x + 1
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: équations du second degrée help
Lostounet a écrit:Tu ne sais pas que, dans une équation, on peut multiplier et diviser les deux cotés par un même nombre?
Et tu ne connais pas la règle de distributivité suivante ? Si au supermarket j'achète deux sachets, avec dans chaque sachet 1 pomme et une poire, alors en tout j'ai:
DEUX(Pomme + Poire) c'est DEUX POMMES + DEUX POIRES
Ben ici c'est pareil, pour tous nombres k, a et b on a k(a + b) = k*a + k*b
Je distribue le (-1):
(-1) *(-x^2 + 2x - 1) = (-1)*(-x^2) + (-1)*(2x) + (-1)*(-1) = x^2 - 2x + 1
D'accord mais le -1 est arbitraire ou on peut prendre 1 autre chiffre?
Et peut on le développer autrement?
En partant de
-x²+2x-1=0
Re: équations du second degrée help
Tu peux prendre (-1), tu peux prendre (+10) tu peux prendre (ma tante) peu importe.
Mais on avait -x^2 + 2x - 1 et toi tu voulais (x^2 ...). le seul moyen d'y parvenir c'est de faire *(-1) pour virer le signe - devant x^2 pour pouvoir factoriser
Mais on avait -x^2 + 2x - 1 et toi tu voulais (x^2 ...). le seul moyen d'y parvenir c'est de faire *(-1) pour virer le signe - devant x^2 pour pouvoir factoriser
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: équations du second degrée help
Lostounet a écrit:Tu peux prendre (-1), tu peux prendre (+10) tu peux prendre (ma tante) peu importe.
Mais on avait -x^2 + 2x - 1 et toi tu voulais (x^2 ...). le seul moyen d'y parvenir c'est de faire *(-1) pour virer le signe - devant x^2 pour pouvoir factoriser
Ok merci de ton aide lostounet.
Une question simple mais qui me pose problème.
Quand tu as
(2x-1)²
pour développer l'expression
(a-b)²
on prend
a=2x
b= -1ou 1
89 messages
- Page 4 sur 5 - 1, 2, 3, 4, 5
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
