équations se ramenant à une équation du second degré
26 messages
- Page 1 sur 2 - 1, 2
équations se ramenant à une équation du second degré
Bonjour, voici mon énoncé :
(E) 6x^4 + 5x^3 - 38x² + 5x + 6 = 0
1/ que constate t-on pour les coefficients ?
=>ils sont positifs et (E) est une fonction polynôme.
0 est-il solution de l'équation (E) ?
=> oui
2/ montrer que (E) équivaut à 6x² + 5x - 38 + 5/x + 6/x² = 0
<=> 6x² + 5x - 38 + 5 + 6 = -1/x² - 1/x² + 1/x² - 1/x
<=> 6x² + 5x - 38 + 5 + 6 + 1/x² + 1/x = 0
<=> 6x² + 5x - 38 + 5/x + 6/x² = 0
3/ poser X = x + 1/x
Montrer que x est solution de (E) si X est solution de 6X² + 5X - 50 = 0 (F)
=> ?? je n'y arrive pas
MERCI de m'aider :happy2:
(E) 6x^4 + 5x^3 - 38x² + 5x + 6 = 0
1/ que constate t-on pour les coefficients ?
=>ils sont positifs et (E) est une fonction polynôme.
0 est-il solution de l'équation (E) ?
=> oui
2/ montrer que (E) équivaut à 6x² + 5x - 38 + 5/x + 6/x² = 0
<=> 6x² + 5x - 38 + 5 + 6 = -1/x² - 1/x² + 1/x² - 1/x
<=> 6x² + 5x - 38 + 5 + 6 + 1/x² + 1/x = 0
<=> 6x² + 5x - 38 + 5/x + 6/x² = 0
3/ poser X = x + 1/x
Montrer que x est solution de (E) si X est solution de 6X² + 5X - 50 = 0 (F)
=> ?? je n'y arrive pas
MERCI de m'aider :happy2:
bonjour;
pour le 2)
si si on réduit au même D:
si on réduit au même D:
on trouve si cette équation à des solutions aucune ne peut-être égale à 0 car on ne peut diviser par 0, d'où la question 1) et il faut remarquer la symétrie des coefficients.
si cette équation à des solutions aucune ne peut-être égale à 0 car on ne peut diviser par 0, d'où la question 1) et il faut remarquer la symétrie des coefficients.
Tu cherches les valeurs de X une fois que tu as trouvé ces 2 valeurs de X tu portes ces valeurs de X et tu cherches x
on trouve

A bientôt.
pour le 2)
si
on trouve
Tu cherches les valeurs de X une fois que tu as trouvé ces 2 valeurs de X tu portes ces valeurs de X et tu cherches x
on trouve
A bientôt.
Bonjour,
Ils sont à égale distance de part et d'autre de ce qui s'apparente à une symétrie.
ce qui s'apparente à une symétrie.
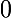 est-il solution?
est-il solution?
Si on a
on a ^n=x^n=0) en portant cette valeur
en portant cette valeur 
}=+6)
on constante que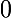 n'est pas solution de l'équation, donc on peut factoriser par
n'est pas solution de l'équation, donc on peut factoriser par 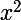 de sorte que l'équation
de sorte que l'équation 
=0)
Comme nest pas solution de lequation, on peut résoudre l équation
nest pas solution de lequation, on peut résoudre l équation

tu peux regarder cela,je termine dans la matinée
A+
1/ que constate t-on pour les coefficients ?
Ils sont à égale distance de part et d'autre de
Si
on constante que
Comme
tu peux regarder cela,je termine dans la matinée
A+
Pour le 1 :
On remarque, que les coefficients sont à équidistance de part et dautre de -38x ce qui sapparente à une symétrie.
x=0 est-il solution de=6x^4 + 5x^3 - 38x^2 + 5x + 6)
E(0)=+6 donc x=0 nest pas solution de E
Pour le 2 :
Donc on peut factoriser suivant les puissances de x, de sorte que léquation
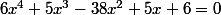
devienne équivalente à :
 =
=) =0
=0
Comme 0 nest pas solution il suffit de résoudre

ce qui ne change rien pour les valeurs de x donnant E=0
Pour le 3 :
Si on pose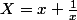
En mettant en facteur par rapport les puissances décroissante de x
 =
=+5(x+\frac{1}{x})-38)
on a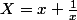 alors
alors 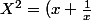^2=x^2+2.x.\frac{1}{x}+\frac{1}{x^2})
= X est dépendant de x
X est dépendant de x

en remplaçant et en identifiant dans :
+5(x+\frac{1}{x})-38=6(X^2-2)+5X-38=0)
=
 On résout alors léquation :
On résout alors léquation :
}{2a})
}{2a})
Avec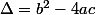 et a=6, b=5, c=-50
et a=6, b=5, c=-50
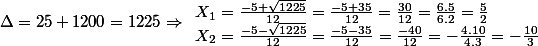 nous savons
nous savons 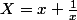 on revient a petit x en donnant les valeurs de X_{1,2}
on revient a petit x en donnant les valeurs de X_{1,2}
en résolvant :
 devient
devient =5x \Rightarrow 2x^2-5x+2=0)
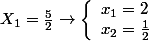
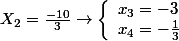
Doù 4 racines qui vérifient léquation de départ
On peut dire que lexposant le plus élevé dans une équation donne le nb de racines.
Lorsquil y a symetrie et que léquation est de la forme on posera
on posera 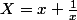
Vous regarder "avec de quoi écrire" et A+ si nécessaire, ce que j'ai fait est correct.
:we:
On remarque, que les coefficients sont à équidistance de part et dautre de -38x ce qui sapparente à une symétrie.
x=0 est-il solution de
E(0)=+6 donc x=0 nest pas solution de E
Pour le 2 :
Donc on peut factoriser suivant les puissances de x, de sorte que léquation
devienne équivalente à :
Comme 0 nest pas solution il suffit de résoudre
ce qui ne change rien pour les valeurs de x donnant E=0
Pour le 3 :
Si on pose
En mettant en facteur par rapport les puissances décroissante de x
on a
=
en remplaçant et en identifiant dans :
=
Avec
en résolvant :
Doù 4 racines qui vérifient léquation de départ
On peut dire que lexposant le plus élevé dans une équation donne le nb de racines.
Lorsquil y a symetrie et que léquation est de la forme
Vous regarder "avec de quoi écrire" et A+ si nécessaire, ce que j'ai fait est correct.
:we:
26 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
