Equation d'une parabole (2points+axe de symétrie)

[cyp68]

Bonjour,

J'ai un exercice de maths à faire, mais je ne m'en sors pas.
Voici l'énoncé : "Donner l'équation de la parabole d'axe de symétrie x=2, et passant par les points A(-1;1) et B(1;4)"
Pourriez-vous me guider pour résoudre cet exercice ?

J'ai essayé avec la forme canonique mais il me manque une donnée.
F(x)=a(x-alpha)^2 + beta
Sachant que les coordonnées du sommet sont (alpha; beta) -> (ici (2; beta)
F(x) = a(x-2)^2+beta
Je remplace ensuite les coordonnées d'un des points. Ici B :
4 = a(1-2)^2 + beta
J'en suis donc à :
4= -2a+beta

Suis-je sur la bonne piste ? Comment dois-je continuer ?
Merci d'avance pour votre aide

[akiwhite]

Je pense que tu peux continuer sur cette piste, fait de même avec A et ...

[vladi]

Bonjour

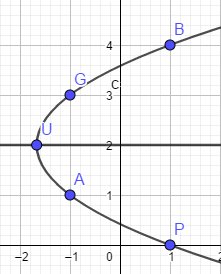
je n'ai pas réalisé la figure avant d'avoir fait les calculs et trouver l'équation

elle est là juste pour aider

un indice : aide toi de la symétrie

[vladi]

mince !!
je me suis trompé d'axe

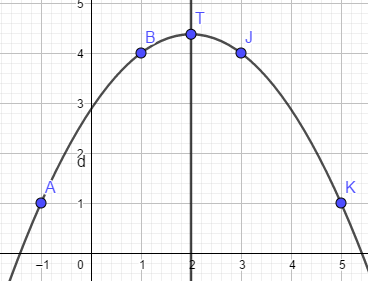mais le principe est le même

[vladi]

je donne un peu plus d'explication

le T de la dernière figure est le sommet de la parabole



cette valeur de

est l'inconnue a de l'équation

en regardant cette figure (la dernière , pas celle d'avant vu que je m'étais trompé d'axe )comprends tu pourquoi?

[cyp68]

Je pense que tu peux continuer sur cette piste, fait de même avec A et ...

Mes calculs précédents sont justes ?

Si je continue avec le point A (-1;1), j'obtiens :
1=a(-1-2)^2 + beta
1=-2a^2 + beta

Comment dois-je continuer ?

[cyp68]

je donne un peu plus d'explication

le T de la dernière figure est le sommet de la parabole



cette valeur de

est l'inconnue a de l'équation

en regardant cette figure (la dernière , pas celle d'avant vu que je m'étais trompé d'axe )comprends tu pourquoi?

Je ne comprends pas comment tu as fait pour trouver le beta de l'axe de symétrie ?
Peux-tu me donner plus d'explications sur la méthode que tu as mis en oeuvre ?

[akiwhite]

Mes calculs précédents sont justes ?

Si je continue avec le point A (-1;1), j'obtiens :
1=a(-1-2)^2 + beta
1=-2a^2 + beta

Comment dois-je continuer ?

Il me semble qu'ils sont bons.

Tu as obtenu deux équations à deux mêmes inconnues , résout un système à deux équations !

[vladi]

Je ne comprends pas comment tu as fait pour trouver le beta de l'axe de symétrie ?
Peux-tu me donner plus d'explications sur la méthode que tu as mis en oeuvre ?

en regardant cette dernière figure tu remarque qu'entre T et B il y a une unité d'écart sur l'axe des abscisses

et entre T et A il y en a trois

et tu remarque qu'entre B et A il y a trois unités d'écart sur l'axe des ordonnées

tu comprend mieux mon équation a(9-1)-3=0 le "a" qui va te permettre de trouver le sommet T et pourquoi il faut ajouter 4 en ordonnées car l'ordonnée de B est en 4 et sa distance en abscisse à T est l'unité?

[cyp68]

Mes calculs précédents sont justes ?

Si je continue avec le point A (-1;1), j'obtiens :
1=a(-1-2)^2 + beta
1=-2a^2 + beta

Comment dois-je continuer ?

Il me semble qu'ils sont bons.

Tu as obtenu deux équations à deux mêmes inconnues , résout un système à deux équations !

Est-ce bien
1=-2a^2 + beta ? ou 1=-4a + beta ?

Mes deux équations sont donc :
1=-4a + beta (eq 1)
4=-4a + beta (eq 2)

Ensuite je fais (eq 2)-(eq 1) et j'obtiens : a=3/8 ?

Mais comment faire pour trouver beta ? Car en résolvant le système d'équation il s'annule ?

[cyp68]

Mes calculs précédents sont justes ?

Si je continue avec le point A (-1;1), j'obtiens :
1=a(-1-2)^2 + beta
1=-2a^2 + beta

Comment dois-je continuer ?

Il me semble qu'ils sont bons.

Tu as obtenu deux équations à deux mêmes inconnues , résout un système à deux équations !

Est-ce bien
1=-2a^2 + beta ? ou 1=-4a + beta ?

Mes deux équations sont donc :
1=-4a + beta (eq 1)
4=-4a + beta (eq 2)

Ensuite je fais (eq 2)-(eq 1) et j'obtiens : a=3/8 ?

Mais comment faire pour trouver beta ? Car en résolvant le système d'équation il s'annule ?

J'ai compris le début de la méthode et je retrouve la même valeur par le calcul du système d'équation (voir autres réponses). Comment dois-je continuer après avoir trouvé a ?

[vladi]

J'ai compris le début de la méthode et je retrouve la même valeur par le calcul du système d'équation (voir autres réponses). Comment dois-je continuer après avoir trouvé a ?

parabole:=

coule de source par translation si tu as compris mon équation a(9-1)-3=0

il faut que tu regarde attentivement la dernière figure et tu verra ça saute aux yeux

[cyp68]

J'ai compris le début de la méthode et je retrouve la même valeur par le calcul du système d'équation (voir autres réponses). Comment dois-je continuer après avoir trouvé a ?

parabole:=

coule de source par translation si tu as compris mon équation a(9-1)-3=0

il faut que tu regarde attentivement la dernière figure et tu verra ça saute aux yeux

J'avoue que j'ai un peu de mal à comprendre la méthode, je m'embrouille en essayant de comprendre.

[cyp68]

Mes calculs précédents sont justes ?

Si je continue avec le point A (-1;1), j'obtiens :
1=a(-1-2)^2 + beta
1=-2a^2 + beta

Comment dois-je continuer ?

Il me semble qu'ils sont bons.

Tu as obtenu deux équations à deux mêmes inconnues , résout un système à deux équations !

Est-ce bien
1=-2a^2 + beta ? ou 1=-4a + beta ?

Mes deux équations sont donc :
1=-4a + beta (eq 1)
4=-4a + beta (eq 2)

Ensuite je fais (eq 2)-(eq 1) et j'obtiens : a=3/8 ?

Mais comment faire pour trouver beta ? Car en résolvant le système d'équation il s'annule ?

Du coup, je remplace beta dans une des équations ?
J'ai essayé de remplacer a par 3/8 dans l'équation 4=-4a+beta
J'obtiens 4= -4*3/8+beta
4 = -3/2 + beta
4 +3/2 = beta
2 + 3/2 = beta
donc beta = 11/2

Mais en voulant vérifier avec l'autre équation je tombe sur un résultat de beta = 5/2
Est-ce normal ? Ai-je fait une erreur de calcul ?

[vladi]

J'avoue que j'ai un peu de mal à comprendre la méthode, je m'embrouille en essayant de comprendre.

parabole:=

tu sais que si l'axe de symétrie est x=0 et que le sommet est en (0,0) ta parabole s'écrit

(avec a<0 ici puisque le sommet possède une valeur d'ordonnée plus grande que les valeurs d'ordonnées des autres points de la parabole)

ça explique le x-2 de ce que j'ai écrit

tu sait que le sommet est en 4+3/8 (l'explication de ça je te l'ai dit tout à l'heure relis là) ça explique pourquoi il faut la soulever de 4+3/8

puis la valeur absolue négative -3/8 s'explique car le sommet possède une valeur d'ordonnée plus grande que les valeurs d'ordonnées des autres points de la parabole

et le coefficient de valeur absolue 3/8 s'explique dans mon explication de l'équation a(9-1)-3=0

expliquée tout à l'heure

[akiwhite]

Oooups désolé de t'avoir induit en erreur en relisant j'ai trouvé ca :

"Je remplace ensuite les coordonnées d'un des points. Ici B :
4 = a(1-2)^2 + beta
J'en suis donc à :
4= -2a+beta "

Or 1-2 = -1 et (-1)² =1
--> 4 = a + Beta

[vladi]

est-ce que tu comprend que le 9 de l'équation
a(9-1)-3=0 vient du fait que la distance en abscisse de T et A de la dernière figure est de trois donc au carré on a 3^2=9
?

[akiwhite]

De plus,

" Si je continue avec le point A (-1;1), j'obtiens :
1=a(-1-2)^2 + beta
1=-2a^2 + beta "

Ici tu t'es carrément gourré !

1 = a(-1-2)² + beta équivaut à 1 = 9a + Beta

car dans a(-1-2)² on priorise le carré et non la multiplication : (-3)²=9

[cyp68]

Oooups désolé de t'avoir induit en erreur en relisant j'ai trouvé ca :

"Je remplace ensuite les coordonnées d'un des points. Ici B :
4 = a(1-2)^2 + beta
J'en suis donc à :
4= -2a+beta "

Or 1-2 = -1 et (-1)² =1
--> 4 = a + Beta

Ah oui effectivement, je me suis trompée dans les priorités.

Donc j'obtiens pour une équation : 4 = a + beta
et pour la seconde 1= 9a + beta
Est ce bien ça ?

Pour continuer je résous un système a deux équations ? et ensuite je remplace beta dans une des formules de départ ? Suis-je sur la bonne voie ?

[vladi]

avec les paraboles il faut comprendre qu'elles transforment des unités perpendiculaires à leurs axes de symétrie en carrés d'unités sur leurs axes de symétrie (si tu comprends ça tu comprends ce que j'ai dit
plus haut)

désolé mais j'ai fait de mon mieux (je vais au lit j'ai sommeil )