équation d'une bissectrice [1ère]
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mathelot
 par mathelot » 07 Jan 2010, 21:32
par mathelot » 07 Jan 2010, 21:32
salut,
trouver l'équation des bissectrices
du couple de droites d'équation
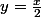
et
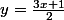
@+
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 07 Jan 2010, 21:46
par oscar » 07 Jan 2010, 21:46
Déterminer d' abord l' angle formé par le couple des bissectrices

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Jan 2010, 22:25
par Ben314 » 07 Jan 2010, 22:25
Bonsoir,
Une autre solution (n'utilisant pas les angles) et de dire que les deux bissectrices sont formées des points M équidistants des deux droites et d'utiliser la formule "calculatoire" de la distance d'un point M:(x,y) à une droite D:ax+by+c=0 qui est d(M,D)=...
P.S. : Je ne sais pas si cette formule est vue en première...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 08 Jan 2010, 08:39
par benekire2 » 08 Jan 2010, 08:39
Ben314 a écrit:Bonsoir,
Une autre solution (n'utilisant pas les angles) et de dire que les deux bissectrices sont formées des points M équidistants des deux droites et d'utiliser la formule "calculatoire" de la distance d'un point M:(x,y) à une droite D:ax+by+c=0 qui est d(M,D)=...
P.S. : Je ne sais pas si cette formule est vue en première...
elle l'est en terminale, mais s'il s'amuse a trouver l'équation d'une bissectrice il doit certainement la connaitre.
Edit: Mathelot me semble être prof ...
-
mathelot
 par mathelot » 08 Jan 2010, 12:57
par mathelot » 08 Jan 2010, 12:57
re,
plus simple ! penser comment déterminer un vecteur directeur..
-
mathelot
 par mathelot » 08 Jan 2010, 20:25
par mathelot » 08 Jan 2010, 20:25
la bissectrice a pour pente

(on norme les vecteurs directeurs

et

et on considère

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités