équation trigonométrique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
adri737
- Messages: 5
- Enregistré le: 10 Jan 2010, 21:28
-
 par adri737 » 10 Jan 2010, 22:27
par adri737 » 10 Jan 2010, 22:27
Bonsoir à tous,
voilà je dois résoudre l'équation suivante :
-2cos(2x)=0)
j'ai procédé comme suit :
=2cos (2x) \Leftright \frac {2sin(2x)cos(2x)} {2cos(2x)}=1 \Leftright sin(2x)=1 \Leftright sin (2x)= \sin \frac {\pi}{2})


et (angles supplémentaires)
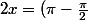 + 2k\pi)

On obtient comme solutions dans l'intervalle
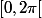
:

Or, j'ai regardé avec un programme traceur de courbe et il manque deux solutions :

et

.
Quelqu'un peut-il me dire où se situe mon erreur?
Merci :we:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 10 Jan 2010, 23:23
par Ben314 » 10 Jan 2010, 23:23
Bonsoir,
Ton erreur, c'est de ne pas avoir traité le cas cos(2x)=0 AVANT de diviser par cos(2x) (je te rapelle qu'on ne peut pas diviser par 0...)
je pense qu'il serait aussi préférable de remplacer le "et" avant "(angles suplémentaires)" par un "ou bien"car l'équation de départ est vérifiée lorsque au moins une des deux formules est vrai.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
 par busard_des_roseaux » 11 Jan 2010, 07:55
par busard_des_roseaux » 11 Jan 2010, 07:55
Bj,
sinon, on peut se ramener à une équation "produit-nul"
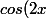 \left( sin(2x)-1 \right) = 0)
ce qui évite de diviser et d'exclure, de facto, des solutions.
-
adri737
- Messages: 5
- Enregistré le: 10 Jan 2010, 21:28
-
 par adri737 » 11 Jan 2010, 08:59
par adri737 » 11 Jan 2010, 08:59
Merci beaucoup pour vos réponses! :id:
quand je fais la règle du produit nul j'obtiens les 4 solutions!
Mais je ne comprends pas vraiment pourquoi le fait de simplifier la fraction "élimine" deux solutions à cette équation (si on considère cos2x non nul)?
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 11 Jan 2010, 09:12
par benekire2 » 11 Jan 2010, 09:12
ben parce que pour commencer y a des cas ou tu divise par 0 et que quand cos2x=0 tu enlève des solutions,
enfin bref, y aurait fallu t'assure que cos2x>0 ce qui est faux
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 11 Jan 2010, 09:13
par benekire2 » 11 Jan 2010, 09:13
regarde l'équation x²=2x
les solutions (triviales) sont 0 et 2
or selon toi quand tu divise par x ça donne x=2 ce qui est faux car, le cas 0 nous embête...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Jan 2010, 11:15
par Ben314 » 11 Jan 2010, 11:15
La méthode donnée par busard_des_roseaux est bien meilleure que celle que tu as commencée à employer (et les calculs sont à peu prés les mêmes).
Conclusion : SI POSSIBLE, dans une équation, éviter de diviser par une quantité dont on n'est pas sûr qu'elle soit non nulle. Et, si on le fait quand même, bien étudier à part le cas où la quantité est nulle.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
