Bonsoir
j'ai un soucis pour mon exercice...
voici l'énoncé:
a)
1 + sin x / cos x = tg ( pi/4 + x/2)
b) On donne cos a = cos a= racine 6 + racine 2 / 4
calculer cos 2 a et en déduire la valeur de l'angle a, supposé aigu.
Merci d'avance pour votre aide
équation trigonométrique
9 messages
- Page 1 sur 1
Salut,
pour le a) :
je suppose qu'il s'agit de démontrer que)
Si c'est le cas n'oublie pas les parenthèses :
1 + sin x / cos x n'est pas pareil que (1 + sin x) / cos x
Pour démontrer l'égalité que je propose on peut utiliser les formules :

= \sin a \cos b + \cos a\sin b)
=\cos a \cos b- \sin a \sin b)
On arrive assez facilement à
 = \frac{\cos(x/2)+\sin(x/2)}{\cos(x/2)-\sin(x/2)})
Puis on mutiplie numérateur et dénominateur par+\sin(x/2))
Et on arrive au résultat avec les formules
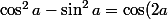)
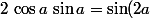)
pour le a) :
je suppose qu'il s'agit de démontrer que
Si c'est le cas n'oublie pas les parenthèses :
1 + sin x / cos x n'est pas pareil que (1 + sin x) / cos x
Pour démontrer l'égalité que je propose on peut utiliser les formules :
On arrive assez facilement à
Puis on mutiplie numérateur et dénominateur par
Et on arrive au résultat avec les formules
Bonsoir
On peut montrer que cos 15 ° = 1/4 ( v6 + v2)
cos 2a = cos 15° et 2a = + ou -
N.B.
cos 30° = 2cos ² 15° -1 = v3/2
En partant de cette relation ,on peut montrer que
cos ² 15°= 1/16( 6+2v12 +2) =.....
Puis en extraire cos 15°
A vous de chercher.
NB On peut auusi partir de cos 15° = 1/4(v6+v2)
Reprendre ensuite le raisonnemenr précédent en ordre INVERSE
Voila la vraie solution.
Continuez...
.
On peut montrer que cos 15 ° = 1/4 ( v6 + v2)
cos 2a = cos 15° et 2a = + ou -
N.B.
cos 30° = 2cos ² 15° -1 = v3/2
En partant de cette relation ,on peut montrer que
cos ² 15°= 1/16( 6+2v12 +2) =.....
Puis en extraire cos 15°
A vous de chercher.
NB On peut auusi partir de cos 15° = 1/4(v6+v2)
Reprendre ensuite le raisonnemenr précédent en ordre INVERSE
Voila la vraie solution.
Continuez...
.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
