équation trigonométrique

[nadine93]

Bonjour,
j'ai vraiment séché sur cette équation, quelqun peut-il m'aider à trouver la solution, merci d'avance:
cos(3x)+sin(x)=1 sur IR.

[nadine93]

Bonjour,
je suis arrivée finalement à résoudre cette équation, j'ai posé t=tan(x/2) et je me suis ramenée à une équation du sixième degré avec 2 solutions évidentes, l'équation du 4ième degré donne 2 valeurs approximatives en utilisant le théorème des valeurs intermédiaires. le logiciel Xcas de tracé de courbe montre bien cela.
J'ai eu le plaisir de partager avec vous cette discussion.

[ThekamikazeFou]

Bonjour,
je suis arrivée finalement à résoudre cette équation, j'ai posé t=tan(x/2) et je me suis ramenée à une équation du sixième degré avec 2 solutions évidentes, l'équation du 4ième degré donne 2 valeurs approximatives en utilisant le théorème des valeurs intermédiaires. le logiciel Xcas de tracé de courbe montre bien cela.
J'ai eu le plaisir de partager avec vous cette discussion.

tu t'ai compliqué la vie, mais si tu es parvenus au résultat, c'est le principale !

[Luc]

tu t'ai compliqué la vie

Je ne vois pas pourquoi?

[nadine93]

moi non plus je ne vois pas pourquoi vous voyez que je me suis compliquée la vie! merci de m'expliquer...

[ThekamikazeFou]

en utilisant les formules de linéarisation et/ou dupplication et/ou addition.
du moin c'est comme ça que j'aurais fais vu que cos (2x + x ) + sin(x) - 1 = 0 etc..
normalement on arrive a une équation de type (cos a ) sin (a) = 0 ou les solutions sont tel que cosa=0 et sina = 0

[nadine93]

Cette étape est obligatoire bien sûr avant de poser t=tan(x/2) mais on n'arrive pas à une équation de la forme (cosa)sina=0, avez-vous essayé pour voir?

[ThekamikazeFou]

Cette étape est obligatoire bien sûr avant de poser t=tan(x/2) mais on n'arrive pas à une équation de la forme (cosa)sina=0, avez-vous essayé pour voir?

1-2sin²(x)cos(x) - 2sin²(x)cos(x) + sin(x) -1 =0
(-4sin²(x)cos(x)) + sin(x) = 0



(j'espere ne pas m'être trompé )

[Kikoo <3 Bieber]

1-2sin²(x)cos(x) - 2sin²(x)cos(x) + sin(x) -1 =0
(-4sin²(x)cos(x)) + sin(x) = 0



(j'espere ne pas m'être trompé )

(1-2sin²(x)) avec des parenthèses au niveau de la 3ème ligne et je pense que ça ira mieux

[ThekamikazeFou]

bon visiblement j'ai fait une erreur de débutant en plus !

[...]
(1-2sin²(x))cos(x) - 2sin²(x)cos(x) + sin(x) -1 =0
cos(x) -4sin²(x)cos(x)) + sin(x)- 1 = 0
cos(x) + sin(x) (-4sin(x)cos(x)) + 1)-1 = 0
cos (x) + sin(x) ( -2sin(2x)+1)-1 = 0

mais effectivement si je n'ai pas le droit e changer ma facon de calculer je vais être vite bloqué ! :)

cos(3x)+sin(x)= 0 aurait été faisable...

[nadine93]

Comme vous voyez il n'y a pas possibilité de continuer sur cette piste, donc la seule façon qui reste est de se ramener à une équation ordinaire.

[ThekamikazeFou]

Comme vous voyez il n'y a pas possibilité de continuer sur cette piste, donc la seule façon qui reste est de se ramener à une équation ordinaire.

Oui, l'équation est simple mais on ne pouvait pas la résoudre avec les formules de trigo.
Mais bon, un petit peu de trigo ne m'a pas fait de mal !

[Anonyme]

@nadine93 et aux élèves en classe de Terminale (et aux autres)

Pour trouver les solutions d'une équation trigonométrique
(exemple l'équation cos(3x)+sin(x)=1 sur IR)

tu as les 2 méthodes suivantes

1) soit étudier la fonction f définie par f(x)=cos(3x)+sin(x)
Fonction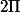 périodique
sur f(x)=1 admet 2 solutions évidentes et
Et les éventuelles autres solutions peuvent être approchées par le théorème des valeurs intermédiaires.

2) soit étudier cos(3x)+sin(x)=1 sur IR comme étant une équation à résoudre
Dans ce cas il y a des règles ( à connaître) sur les différents changements de variable qui sont envisageables
Remarque
Le changement de variable permet en général de s'en sortir malgré qu'il complique souvent les calculs

Voici quelques questions (dans le but de faire cogiter un tout petit peu...)
Question 1 : Expliquer pourquoi le changement de variable est envisageable
Question 2 : Quels sont les autres changements de variable possibles (et suite à quelles règles ?)
Question 3 : Connais tu d'autres méthodes , si oui peux tu les citer ( par exemple on peut citer résolution via des astuces provenant des formules trigonométriques courantes )

Dans l'attente de lire vos réponses
A+

[nadine93]

Merci d'abord pour vos remarques intéressantes.
je vois personnellement une seule formule trigonométrique à part : t=tan(x/2) qui pourrait être une piste de résolution: c'est : cosa+sinb=...
Sinon, avez-vous d'autres suggestions?
A+