Montrer que
Equation
18 messages
- Page 1 sur 1
Equation
Bonsoir, je bloque sur cette question.
Montrer que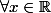 l'équation
l'équation =x) possède au moins une solution si et seulement si
possède au moins une solution si et seulement si 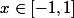
Montrer que
Re: Equation
D où :
S il existe
Alors
Modifié en dernier par mathelot le 03 Jan 2019, 14:16, modifié 2 fois.
Re: Equation
Pour la réciproque, =-1 \text{ et } sin(\frac{\pi} {2})=1) . La fonction sin() est continue et prend donc toutes les valeurs entre-1 et 1, d'après le TVI.
. La fonction sin() est continue et prend donc toutes les valeurs entre-1 et 1, d'après le TVI.
si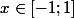
il existe alors tel que
tel que
 =x)
si
il existe alors
Modifié en dernier par mathelot le 03 Jan 2019, 14:23, modifié 2 fois.
Re: Equation
mehdi-128 a écrit:Bonsoir, je bloque sur cette question.
Montrer quel'équation
possède au moins une solution si et seulement si
Ce n'est pas difficile à voir graphiquement.
La droite y=C avec C une constante coupe la courbe y=sin(t) uniquement lorsque C est entre -1 et 1.
Et quand elle la coupe en un point elle la coupe en une infinité.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Equation
Merci pour vos réponses je voulais savoir si ma rédaction est juste :
Notons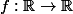 ,
, = \sin (\theta))
Soit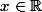 .
.
=x) admet une solution si et seulement si
admet une solution si et seulement si ) si et seulement si
si et seulement si 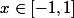
Notons
Soit
Re: Equation
La question ne devrait même pas se poser. Evidemment que la réponse est non.
Et je ne dirai pas pourquoi. En effet de multiples fois je t'ai expliqué que cela ne faisait pas de poser la même question simultanément sur différents forums. Ou alors tu ne comprends rien ou alors tu te moques du monde.
Et je ne dirai pas pourquoi. En effet de multiples fois je t'ai expliqué que cela ne faisait pas de poser la même question simultanément sur différents forums. Ou alors tu ne comprends rien ou alors tu te moques du monde.
Re: Equation
Alors je réexplique. Poser la même question simultanément sur plusieurs forums, ça implique qu'on va perdre son temps à t'expliquer quelque chose qui est déjà fait ailleurs (je te rappelle qu'on est bénévole).
D'autre part je trouve que depuis que tu travailles à un niveau bac + quelque chose, tes questions sont la plupart du temps hyper basiques voire d'une évidence absolue. Sur un message précédent tu a aussi demandé (sur au moins 2 forums) comment on résout x^n =0 (avec x dans R^+ et n entier).
Alors que le principe du raisonnement c'est de tenir un discours qui fait que les personnes qui ont quelque chose entre les 2 oreilles soient d'accord avec l'affirmation qui ne doit pas être trop banale.
Il s'avère que l'exercice ici est disons basique (niveau bac - 1 donc en dessous de ton niveau) . Ton discours (ta preuve) tient en une seule phrase mal fagotée
( deux ssi dans une phrase!, c'est plutôt pas joli) dans laquelle il n'y a pas la justification de Im(f)=[-1,1]. Tu ne justifies pas ce que tu veux justifier et tu demande si c'est correct, c'est tout de même fort.
la fonction sinus est archi connue à bac -1. Donc à bac+ 1, il n'y a rien à démontrer c'est évident. Mais si tu veux donner une démo alors la moindre des choses c'est d'expliquer la seule chose explicable, c'est à dire que Im(f)=[-1,1].
D'autre part je trouve que depuis que tu travailles à un niveau bac + quelque chose, tes questions sont la plupart du temps hyper basiques voire d'une évidence absolue. Sur un message précédent tu a aussi demandé (sur au moins 2 forums) comment on résout x^n =0 (avec x dans R^+ et n entier).
Alors que le principe du raisonnement c'est de tenir un discours qui fait que les personnes qui ont quelque chose entre les 2 oreilles soient d'accord avec l'affirmation qui ne doit pas être trop banale.
Il s'avère que l'exercice ici est disons basique (niveau bac - 1 donc en dessous de ton niveau) . Ton discours (ta preuve) tient en une seule phrase mal fagotée
( deux ssi dans une phrase!, c'est plutôt pas joli) dans laquelle il n'y a pas la justification de Im(f)=[-1,1]. Tu ne justifies pas ce que tu veux justifier et tu demande si c'est correct, c'est tout de même fort.
la fonction sinus est archi connue à bac -1. Donc à bac+ 1, il n'y a rien à démontrer c'est évident. Mais si tu veux donner une démo alors la moindre des choses c'est d'expliquer la seule chose explicable, c'est à dire que Im(f)=[-1,1].
Re: Equation
Ce qui me trouble dans ce qu'écrit Mehdi, c'est que la variable  est liée à x dans l'équation
est liée à x dans l'équation
=x) et par contre , elle est libre dans la flèche
et par contre , elle est libre dans la flèche )
Re: Equation
Aviateur, je travaille sur le début du programme de MPSI, mais j'ai arrêté ma scolarité il y a longtemps donc parfois je pose des questions niveau première terminale, j'ai oublié certaines choses.
Je ne me souviens plus de comment justifier que := [-1,1])
Salut Mathelot je ne vois pas de problème la fonction est)) qui dépend de
qui dépend de  et
et  un paramètre.
un paramètre.
J'ai compris votre solution avec le TVI. Merci.
Je ne me souviens plus de comment justifier que :
Salut Mathelot je ne vois pas de problème la fonction est
J'ai compris votre solution avec le TVI. Merci.
Re: Equation
mehdi-128 a écrit:
Salut Mathelot je ne vois pas de problème la fonction estqui dépend de
et
un paramètre.
.
quand on écrit
Par contre, quand on écrit
perso, j'aurai pris une autre lettre que
Re: Equation
Ah d'accord j'ai compris votre remarque en effet le  qui vérifie
qui vérifie =x) dépend de
dépend de 
J'aurais pu définir :=\sin(y))
J'aurais pu définir :
Re: Equation
Ben ça dépend de ce que tu sais sur la fonction sin / de comment tu la définis etc...
Si tu sais que sin est continue et comprise entre -1 et 1 (par exemple via la représentation sur le cercle trigo) le théorème des valeurs intermédiaire et deux points bien choisit te donne la solution.
Si tu prends la def de sin comme série entière ça va être plus délicat...
Si tu sais que sin est continue et comprise entre -1 et 1 (par exemple via la représentation sur le cercle trigo) le théorème des valeurs intermédiaire et deux points bien choisit te donne la solution.
Si tu prends la def de sin comme série entière ça va être plus délicat...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: Equation
@Sylviel
Dans mon livre de MPSI il est écrit que la définition de la fonction cos et sin sera vu en deuxième année. Donc ici j'ai juste la définition avec le cercle trigo.
J'ai compris la démo de Mathelot pour la réciproque.
Maintenant j'aimerais montrer que si l'équation=x) possède une solution alors forcément
possède une solution alors forcément 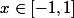
Je vois pas trop comment faire même si ça m'a l'air évident.
Dans mon livre de MPSI il est écrit que la définition de la fonction cos et sin sera vu en deuxième année. Donc ici j'ai juste la définition avec le cercle trigo.
J'ai compris la démo de Mathelot pour la réciproque.
Maintenant j'aimerais montrer que si l'équation
Je vois pas trop comment faire même si ça m'a l'air évident.
Re: Equation
-1 <= sin(theta) <= 1
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 147 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :


