Equation second degré

par **destoyeur** » 02 Juin 2007, 16:29

Bonjours à tous!

Je suis Suisse et en dernière année d'école obligatoire(Je ne sais pas a quoi cela correspond en France). Je ne sais pas si c'est bien ici que je dois donc posté...

Dans une semaine je commence mes examen pour obtenir mon certif.
En Mathematique je suis plutôt doué avec une moyenne annuel de 5.5/6 mais j'avoue que pour les equations 2e degré + celle avec fraction je ne comprend pas bien.

Donc les équations sont:

x-2/3=3x+1/2

x(au carré) -x-20=0

Est-ce que quelqu'un peux résoudre ces equations et m'expliquer chaque étape?

Je vous remerci d'avance!

par **anima** » 02 Juin 2007, 16:34

destoyeur a écrit:Bonjours à tous!

Je suis Suisse et en dernière année d'école obligatoire(Je ne sais pas a quoi cela correspond en France). Je ne sais pas si c'est bien ici que je dois donc posté...

Dans une semaine je commence mes examen pour obtenir mon certif.
En Mathematique je suis plutôt doué avec une moyenne annuel de 5.5/6 mais j'avoue que pour les equations 2e degré + celle avec fraction je ne comprend pas bien.

Donc les équations sont:

x-2/3=3x+1/2

Celle la est du premier degré. C'est normal?

x(au carré) -x-20=0

Avec delta:

Avec une forme cannonique:

(J'étais d'assez bonne humeur pour faire les 2 méthodes

par **destoyeur** » 02 Juin 2007, 16:36

oui! c'est normal!

par **anima** » 02 Juin 2007, 16:41

destoyeur a écrit:oui! c'est normal!

Je développe au maximum pour que tu voies exactement ce que je fais.

par **destoyeur** » 02 Juin 2007, 16:44

Euh... par contre moi j'ai jamais appris avec delta ou cannonique :triste:
(En suisse on fait tout différent)

mois j'ai appris comme ca: ex.

-3x-4+6x=x-10 { on passe le -4 de l'autre coté du = il devient donc +4
-3x+6x=x-6 {on passe le x de l'autre coté du = il devient donc -x
2x=-6 { divisé par 2
x=-3

Ma méthode me semble plus simple.

par **anima** » 02 Juin 2007, 16:51

destoyeur a écrit:Euh... par contre moi j'ai jamais appris avec delta ou cannonique :triste:
(En suisse on fait tout différent)

mois j'ai appris comme ca: ex.

-3x-4+6x=x-10 { on passe le -4 de l'autre coté du = il devient donc +4
-3x+6x=x-6 {on passe le x de l'autre coté du = il devient donc -x
2x=-6 { divisé par 2
x=-3

Oui oui, ca c'est du premier degré. Delta ou la forme cannonique, c'est pour le second degré (x^2)

par **destoyeur** » 02 Juin 2007, 16:55

J'ai un vague souvenir d'un calcul comme ca mais je ne sait pas s'il est juste :s

x(au carré)-x-20=0

(x+4)(x-5)=0

en fait on le modifie pour qu'il devienne au 1er degré :) il est juste mon calcul :)

par contre apres je ne sais pas comment le résoudre :s

par **destoyeur** » 02 Juin 2007, 17:04

je trouve x(au carré) =1

par **nico74** » 02 Juin 2007, 17:05

Une équation du secon degré posede une, deux ou zero solutions.

Cherche tout d'abord une solution évidente (1,2,3,4,5,...) s'il y en a.

C'est bon ! On voit que

.
Donc 5 est solution. On va chercher l'autre s'il yen a une.

Sache que une équation du second du second degré

a deux solutions si et seulement si on peut la mettre sous la forme

avec

et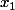

les dex solutions.

Ici on a

.
D'où

On developpe à gauche

Enfin, on dit que deux polynomes sont égaux s ils ont les memes coefficients, c'est a dire

Ce qui nous donne

On a donc deux solutions : -4 et 5

par **nico74** » 02 Juin 2007, 17:08

Ton calcul n'est pas détayé, comment tu trouves la forme factorisée.

Après, avec ta forme factorisée, tu dis qu un produit est nul si l un de tes facteurs est nul.

Doncon a soit (x+4)=0 ou (x-5)=0

par **destoyeur** » 02 Juin 2007, 17:12

Je suis désolé mais j'y comprend rien :S

Je pense qu'il faut que je demande a mon professeur lundi... qu'il m'explique comme il nous a expliquer depuis le début parce que la ^^'

En tout cas merci quand meme pour tes réponse je vais essayer de comprendre ca ce soir :)

Je sais que nous sommes dans un forum de math mais j'ai une question est-ce que tu es aussi douer en allemand et en anglais qu'en math? :zen:
Parce que j'ai deux texte de présentation oral (1 en ang et 1 en all) + un texte de description d'un objet en all

à faire lire au moins savoir si ca veux dire quelque chose...

sinon pas grave!

par **destoyeur** » 02 Juin 2007, 17:18

Voila je crois avoir posté au bonne endroit :
http://www.maths-forum.com/showthread.php?p=223455#post223455

par **oscar** » 02 Juin 2007, 17:21

Bonjour

Peut-être que pour x² - x - 20 =0,
tu cherches 2 nombres dont le produit est -20 et la somme -1
On trouve - 5 et + 4
Ce qui donne (x - 5) ( x + 4) =0
Donc x-5=0 <=> x= 5
ou x + 4 = 0 <=> x = -4

par **nico74** » 02 Juin 2007, 17:25

Ca me semble bien ça Oscar !!! S'il n a pas vu le discriminant, je ne pense pas que les solutions soient compliquées (pour ne pas dire complexes :we: )

Car ca marche si nos solutios sont entières, pour trouver les diviseurs de -20 et les multiplier entre eux

par **destoyeur** » 02 Juin 2007, 17:29

Ce que dit oscar ma l'air trop simple pour que ce soit juste xD
mais ca marche quand meme o_O enfin si ca marche dans tout les cas avec un x(au carré) et bien j'ai compris

par **nico74** » 02 Juin 2007, 17:39

THEOREME GENERAL :

Les solutions

et

de l'équation

vérifient :

et

par **destoyeur** » 02 Juin 2007, 17:41

ca repart en chinois ^^'

SVP partez du principe que je suis un peu con :)

par **oscar** » 02 Juin 2007, 18:23

Cela correspond à la formule
x² - S x + P=0 tirées de la forme ax² +bx +c=0<=>a(x² + b/a x + c/a) =0

Avec S =-b/a et P = c/a méthode utilisées pour trouver les racines

par **nico74** » 02 Juin 2007, 18:26

Exemple :

Quelles sont les solutions de

.

Les couples dont le produit vaut -18 sont

(-1,18), (1,-18), (-2,9), (2,-9), (-6,3), (6,-3)

Après tu regardes la somme des éléments des couples.Le bon est celui qui donne -(-3)=3

-1+18=17 non
1-18=-17 non
-2+9=7 non
2-9=-7 non
-6+3=-3 non
6-3=3 OK

Tes solutions sont donc 6 et -3

par **destoyeur** » 02 Juin 2007, 22:31

Nico je t'ai compris c'est ca que le prof nous avait appris!

Equation second degré

Equation second degré

Qui est en ligne