Equation incompréhensible :s

[etigau]

Bonjour, dans un exo on me demande :

1)Montrer que,pour a différent de 0, on a:

ax²+bx+c= a[(x+ b/2a)²- (b²-4ac)/4a²]

2) Utiliser ce résultat pour résoudre les équations:

a) 2x²+x-15=0

b) 2x²-11x-6=0

Voila je suis en seconde j'ai aucune idée de comment résoudre ça, je suis allé sur wiki et j'ai trouver un truc qui me semble être la solution: calculer avec le discriminant, mais j'ai jamais utilisé ça et j'ai rien compris... de toute façon mon prof de math est un fou furieux y nous donne tous le temps des truc à faire qu'on s'est pas faire xD. Heureusement qu'il existe se genre de forum. Merci de votre aide.

[Clembou]

Bonjour, dans un exo on me demande :

1)Montrer que,pour a différent de 0, on a:

ax²+bx+c= a[(x+ b/2a)²- (b²-4ac)/4a²]

2) Utiliser ce résultat pour résoudre les équations:

a) 2x²+x-15=0

b) 2x²-11x-6=0

Voila je suis en seconde j'ai aucune idée de comment résoudre ça, je suis allé sur wiki et j'ai trouver un truc qui me semble être la solution: calculer avec le discriminant, mais j'ai jamais utilisé ça et j'ai rien compris... de toute façon mon prof de math est un fou furieux y nous donne tous le temps des truc à faire qu'on s'est pas faire xD. Heureusement qu'il existe se genre de forum. Merci de votre aide.

Oui, en fait, c'est l'introduction au calcul de discriminants qu'on fait normalement en première S. Ton prof te demande vraiment des choses difficiles. On trouve la réponse à la question 1 sur ce poly :

http://pagesperso-orange.fr/gilles.costantini/Lycee_fichiers/CoursP_fichiers/dg2.pdf

[etigau]

Merci beaucoup je vais lire se que tu m'a donner.

[etigau]

Ba... j'ai lu mais j'ai vraiment du mal à tous comprendre. S'est un dm pour demain, personne dans ma classe n'a réussi cette exo, et il n'y à que 2 exo dans son dm... on est un peu tous dans le pétrin, si une bonne âme pouvait ... pas me donné la réponse, mais bien m'aider, ça serait simpa. Pasque les histoire de delta etc... j'ai rien compris :p

[annick]

Bonsoir,
effectivement, en seconde tu n'es pas sensée connaître le discriminant.
Pour la première question, deux solutions:
La première facile, où tu redéveloppes l'expression à droite du signe = et tu dois retomber sur ax²+bx+c
La deuxième plus difficile où tu pars de l'expression de gauche et tu factorises :

ax²+bx+c=a(x²+ b/a x + c/a)

Or x² + b/a x peut être considéré comme le début d'une identité remarquable

(x+b/2a)², mais dans laquelle on n'a pas (b/2a)²( le troisième terme de l'identité remarquable). Il va donc falloir déduire (b/2a)², ce qui donne

ax²+bx+c= a[(x+b/2a )² - ((b/2a)² +c/a]

ax²+bx+c= a[(x+ b/2a)² - (b²+4ac)/(4a²)] (en mettant juste au même dénominateur)

J'espère que tu comprendras, mais en seconde, la première méthode suffit peut-être.
Je regarde la suite, à bientôt

[annick]

Ensuite ce sont des applications numériques : dans ta formule de droite pour la 1ère équation, tu remplaces a par 2, b par 1 et c par -15 et tu verras que tout s'arrange bien pour que tu trouves la solution

[Cheche]

Salut etigau et annick, je me permet de faire une petite correction.

x² + b/a x est le début d'une identité remarque qui est : (x+b/(2a) )² et non (x+b/a )²

(a+b)² = a² + 2ab + b²

[annick]

Merci Cheche pour ta remarque. Effectivement j'avais fait cette petite étourderie que j'ai en partie corrigée, mais j'en avais encore laissé passer un bout. Je corrige tout de suite en rouge pour bien marquer ma honte.

[fibonacci]

bonjour;



on cherche une factorisation de




on a





d'où




et

[Cheche]

Salut,

Bon je pense que tu as du faire la question 1.

Sinon pour la question 2,

2x²+x-15=0
2 * ( x² +x/2 - 15/2 ) = 0
2 *( (x+1/4)² -15/2 -1/16 ) = 0
2 *( (x+1/4)² -121/16 ) = 0
2 *( (x+1/4)² - (11/4)² ) = 0

... ensuite tu fais une belle identité remarque a² - b² et tu vas avoir le trinome du second degré de la forme c(x-a)(x-b) => les racines sont donc a et b.

Voilà et tu fais de même pour l'autre équation.

REMARQUE : Juste une petite remarque sur le cours que tu verras en première, en réalité, tu es entrain d'utiliser la démonstration sur la résolution des trinômes.

2x²+x-15=0 ax² +bx+c=0
En gros pour résumé, le discriminant (delta) de cette équation est : b² - 4*ac = 121, tu le retrouves dans ma démonstration.

- Si delta > 0 Alors en peux utiliser a² - b² est trouver deux solutions réels.
- Si delta =0 Alors tu es dans le cas d'un carré parfait, donc une racine (double)
- Si delta Pas de solution réel.

[busard_des_roseaux]

Bonjour,

Il y a de nombreuses classes de Seconde où l'on commence à étudier
l'équation du second degré,vers la fin d'année. :doh:

Il aurait été sans doute plus "pédagogique" de traiter dans l'ordre les équations



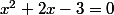à écrire



pour vous faire piger le truc progressivement...