[1ereS] dm équation de cercle

[coralyne]

Bonjour, j'ai un dm pour lundi et je suis bloquer dans ma démarche ...
L'énoncé est :

Trouvez une équation de cercle C circonscrit au triangle ABC avec A(2;0), B(0;3) et C(3;4).

Sur un croquis, j'ai construit les médiatrices de chaque côté du triangle ABC (voir image).Les médiatrices coupent donc chaque segment en leur milieu. J'ai donc calculer les milieux de chaque segment : (ex: soit N, le milieu de [BC] a pour coordonnées: xN=(xB+xC)/2=(0-3)/2=1.5 et yN=(yB+yC)/2=(3+4)/2=3.5 donc N(1.5;3.5) ) j'ai fait de même pour K milieu de [AC] et D milieu de [BA] et g trouver K(2.5;2) et D(1;1.5).
Après avoir calculer les coordonnées de chaque milieu de segment, j'ai calculer l'équation de deux médiatrices: la médiatrice (m) qui coupe [BC] en N et (m') qui coupe [AB] en D.
j'ai donc fait pour (m):
a= (yC-yB)/(xC-xB)= (4-3)/(3-0)= -1/3
N appartenant à [BC], ses coordonnées en vérifient l'équation:
y= ax+b
3.5=(-1/3)*1.5+b
3.5=-0.5+b
3.5+0.5=b
4=b
d'où l'équation y=-1/3x+4
j'ai fait de même pour (m') et j'ai trouver y=-3/2x+3.
Ensuite j'ai fait un système d'équation pour calculer les coordonnées de I, le centre du cercle:
y=-1/3x+4 (1)
y=-3/2x+3 (2)
(1)=(2)
-1/3x+4=-3/2x+3
-1/3x+3/2x=3-4
7/6x=-1
x=-6/7
J'ai remplacer x par sa valeur dans une des deux équations du départ:
y=(-1/3)*(-6/7)+4
y=30/7
Ainsi on a: I(-6/7;30/7)
OR c'est la que vient mon problème, en vérifiant les coordonnées de I, en calculant les équations de deux autres médiatrices (par exemple celle qui coupe [AC] en K et (m)),je ne trouve pas du tout les mêmes coordonnées de I;dans l'exemple que je vient de donner, je trouve I(3.6;4.2) ce n'est pas normal !?
Aidez-moi s'il vous plait

[img]20150508_171201[/img]

[Carpate]

Bonjour, j'ai un dm pour lundi et je suis bloquer dans ma démarche ...
L'énoncé est :

Trouvez une équation de cercle C circonscrit au triangle ABC avec A(2;0), B(0;3) et C(3;4).

Sur un croquis, j'ai construit les médiatrices de chaque côté du triangle ABC (voir image).Les médiatrices coupent donc chaque segment en leur milieu. J'ai donc calculer les milieux de chaque segment : (ex: soit N, le milieu de [BC] a pour coordonnées: xN=(xB+xC)/2=(0-3)/2=1.5 et yN=(yB+yC)/2=(3+4)/2=3.5 donc N(1.5;3.5) ) j'ai fait de même pour K milieu de [AC] et D milieu de [BA] et g trouver K(2.5;2) et D(1;1.5).
Après avoir calculer les coordonnées de chaque milieu de segment, j'ai calculer l'équation de deux médiatrices: la médiatrice (m) qui coupe [BC] en N et (m') qui coupe [AB] en D.
j'ai donc fait pour (m):
a= (yC-yB)/(xC-xB)= (4-3)/(3-0)= -1/3
N appartenant à [BC], ses coordonnées en vérifient l'équation:
y= ax+b
3.5=(-1/3)*1.5+b
3.5=-0.5+b
3.5+0.5=b
4=b
d'où l'équation y=-1/3x+4
j'ai fait de même pour (m') et j'ai trouver y=-3/2x+3.
Ensuite j'ai fait un système d'équation pour calculer les coordonnées de I, le centre du cercle:
y=-1/3x+4 (1)
y=-3/2x+3 (2)
(1)=(2)
-1/3x+4=-3/2x+3
-1/3x+3/2x=3-4
7/6x=-1
x=-6/7
J'ai remplacer x par sa valeur dans une des deux équations du départ:
y=(-1/3)*(-6/7)+4
y=30/7
Ainsi on a: I(-6/7;30/7)
OR c'est la que vient mon problème, en vérifiant les coordonnées de I, en calculant les équations de deux autres médiatrices (par exemple celle qui coupe [AC] en K et (m)),je ne trouve pas du tout les mêmes coordonnées de I;dans l'exemple que je vient de donner, je trouve I(3.6;4.2) ce n'est pas normal !?
Aidez-moi s'il vous plait

[img]20150508_171201[/img]

tu peux utliser l'équation du cercle de centre I(a,b) et de rayon r :
et l'appliquer aux points A, B, C
--> système de 3 équations à 3 inconnues

[coralyne]

Je ne sais pas faire les équations à 3 inconnues ...
En regardant des exemples sur internet, je ne vois pas comment faire, puisque sur internet, il y 3 inconnues (x,y,z) or dans mon exo, j'en ai deux ...

[siger]

bonjour,

pas evident de comprendre ce que tu as fait!

1- a tel que tu le definis est le coefficient directeur de (BC)
or le centre du cercle est sur la mediatrice de (BC) donc sur une droite dont le coefficient directeur est -1/a (droite perpendiculaire) et non a
l'equation est donc de la forme y = -x/a + b
....
2- le calcul de a comporte une erreur : a = 1/3 et non -1/3

l'equation de la mediatrice de (BC) est y = -3x +13/2 (a verifier)

........

[coralyne]

oui, c'est vrai que c difficile de comprendre.. et effectivement, j'ai fait une erreur dans le calcul de a.
J'ai essayer de faire l'équation de la médiatrice de [BC] avec la forme que vous m'avait donné et j'ai trouvé
y=-x/(1/3)+8

[Ben314]

Salut,
Moi aussi je suis "une bille" en calcul, donc, ce que je te suggérerais de faire, c'est de vérifier le plus possible d'étapes de ton calcul.
Par exemple, c'était très judicieux de regarder si le point que tu trouve était (ou pas) sur la dernière médiatrice.

Donc, fait un dessin, si possible sur du papier à petit carreau, en prenant une échelle assez grande et trace le plus précisément possible les médiatrices et vérifie (avec un compas) que tu as bien le centre du cercle circonscrit.
Ensuite, tu as du voir comment on "lit" sur un dessin l'équation d'une droite : si c'est y=ax+b, où "lit-on" le a ? le b?
Ca te permettra de vérifier une par une que les droites dont tu as calculé les équation sont les bonnes (tu peut aussi, prendre un peu au pif un (x,y) qui vérifie l'équation et regarder sur le dessin s'il est (à peu près...) sur la droite en question).

EDIT : un petit "coup de pouce" : la médiatrice de [BC] a effectivement pour équation y=-x/(1/3)+8 qui peut s'écrire plus simplement (ça vaut quoi 1/(1/3) ?)

Sinon, si tu ne te rappelle plus comment on trouve le coefficient directeur de la médiatrice de deux points B et C, tu as toujours la solution de dire que les points M qui sont sur la médiatrice sont ceux tels que d(M,B)=d(M,C), c'est à dire
(x-xB)²+(y-yB)²=(x-xC)²+(y-yC)².
C'est pas forcément ni le plus subtil, ni le plus rapide, mais ça vaut toujours mieux que d'écrire une connerie... :zen:

[Romanouch]

Salut Coralyne,

Je trouve que ta méthode est bonne.

Par contre, c'est ta méthode pour calculer l'équation des droites (m) et (m') qui n'est pas correcte.
Tu écris que

d'où vient cette formule? Elle est fausse.
Si tu es en 1eS, vous êtes sans doute en train de faire le produit scalaire, et notamment son utilisation pour calculer l'équation d'une droite perpendiculaire à une autre. Si c'est bien le cas, regarde ton cours concernant les vecteurs directeurs, ça devrait t'aider.

Puisque tu as déjà bien avancé et que Siger t'a donné une réponse fausse, je te donne la bonne équation pour (m):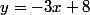

Essaie de la retrouver par toi-même puis de trouver l'équation de (m').

[siger]

re

mille excuses
en effet ce serait nouveau si 9 + 7 etait egal a 13 , meme si je l'ai ecrit ...'.
ah, les petits brouillons sur un coin de table!

[coralyne]

Salut,
Moi aussi je suis "une bille" en calcul, donc, ce que je te suggérerais de faire, c'est de vérifier le plus possible d'étapes de ton calcul.
Par exemple, c'était très judicieux de regarder si le point que tu trouve était (ou pas) sur la dernière médiatrice.

Donc, fait un dessin, si possible sur du papier à petit carreau, en prenant une échelle assez grande et trace le plus précisément possible les médiatrices et vérifie (avec un compas) que tu as bien le centre du cercle circonscrit.
Ensuite, tu as du voir comment on "lit" sur un dessin l'équation d'une droite : si c'est y=ax+b, où "lit-on" le a ? le b?
Ca te permettra de vérifier une par une que les droites dont tu as calculé les équation sont les bonnes (tu peut aussi, prendre un peu au pif un (x,y) qui vérifie l'équation et regarder sur le dessin s'il est (à peu près...) sur la droite en question).

EDIT : un petit "coup de pouce" : la médiatrice de [BC] a effectivement pour équation y=-x/(1/3)+8 qui peut s'écrire plus simplement (ça vaut quoi 1/(1/3) ?)

Sinon, si tu ne te rappelle plus comment on trouve le coefficient directeur de la médiatrice de deux points B et C, tu as toujours la solution de dire que les points M qui sont sur la médiatrice sont ceux tels que d(M,B)=d(M,C), c'est à dire
(x-xB)²+(y-yB)²=(x-xC)²+(y-yC)².
C'est pas forcément ni le plus subtil, ni le plus rapide, mais ça vaut toujours mieux que d'écrire une connerie... :zen:

J'ai fait un croquis sur du papier millimétré avec comme échelle 1 unité= 2 carreaux: j'ai fait mon répère, placer mes points A,B et C, tracer mes médiatrices, et tracer mon cercle circonscrit (vu que l'intersection des médiatrices me donne le centre du cercle). J'ai ensuite tenter de "lire" le coefficient directeur et l'ordonnée à l'origine mais je trouve des résultats bizarre par exemple, pour le coefficient directeur, je trouve -2.7 alors que par les calculs je trouve 1/3 ....
J'ai ensuite essayer la formule que vous m'avez donner mais je l'a comprend pas, les x et y, il faut les laisser tels quels ou les changer par les coordonnées du point sur la médiatrice ?
En ce qui concerne votre petit "coup de pouce", 1/(1/3) vaut 3

[siger]

re

il semble que tu confondes les choses
1- le coefficient directeur de la droite BC est 1/3 comme tu l'as calculé
2- le centre du cercle est sur la mediatrice de BC, donc sur une droite perpendiculaire a BC de coeffient directeur -3
( ou bien tu connais la propriete : a et b coefficients de deux perpendiculaires sont lies par la relation a*b = -1,
ou bien tu ecris que le vecteur directeur V de la mediatriice et BC ont un produit scalaire nul (V.BC=0)

[Ben314]

Oui : 1/(1/3)=3 et ton équation :

...et j'ai trouvé y=-x/(1/3)+8

qui se simplifie en y=-3x+8 était tout à fait correcte. Après, si ton -2.7 lu sur le dessin correspond à la pente de la médiatrice de [BC], tu n'est pas si loin du compte que ça vu que par le calcul tu as trouvé un coefficient directeur de -3 (c'est vrai que ça fait quand même une erreur "non négligeable" de 3mm...)

Sinon, concernant l'équation (x-xB)²+(y-yB)²=(x-xC)²+(y-yC)², le x et le y, ben tu les garde "tels quels" : c'est exactement la même chose que quand tu écrit que l'équation d'une droite est (par exemple) y=3x+5 : x et y tu ne sait pas du tout combien il valent. Par contre, si on te donne les coordonnées x et y d'un point M, ça te permet immédiatement par un simple calcul de savoir si M est ou pas sur la droite.
Ben là, c'est pareil : on sait qu'un point M de coordonnées x et y est sur la médiatrice de BC] lorsque (x-xB)²+(y-yB)²=(x-xC)²+(y-yC)².
On pourrait effectivement directement remplacer (par exemple) x par 3 et y par 7 puis regarder si c'est vrai ou pas pour savoir si le point de coordonnées (3,7) est ou pas sur la médiatrice, mais il est bien plus malin de simplifier l'expression le plus possible en gardant les lettres x et y pour ensuite pouvoir vérifier bien plus rapidement si des points sont ou pas sur la médiatrice.

Ici, ça aurait donné
(x-0)^2+(y-3)^2=(x-3)²+(y-4)²
x²+y²-6y+9=x²-6x+9+y²-8y+16
8y-6y=-6x+16
y=-3x+8
et, heureusement, on trouve le même résultat qu'avec l'autre méthode.

Mais je le REDIT, ça semble être une autre méthode que celle attendu (l'intérêt, c'est qu'on peut l'appliquer même si on a "oublié" le calcul du coeff directeur d'une droite orthogonale à une droite donnée)

[coralyne]

Salut Coralyne,

Je trouve que ta méthode est bonne.

Par contre, c'est ta méthode pour calculer l'équation des droites (m) et (m') qui n'est pas correcte.
Tu écris que

d'où vient cette formule? Elle est fausse.
Si tu es en 1eS, vous êtes sans doute en train de faire le produit scalaire, et notamment son utilisation pour calculer l'équation d'une droite perpendiculaire à une autre. Si c'est bien le cas, regarde ton cours concernant les vecteurs directeurs, ça devrait t'aider.

Puisque tu as déjà bien avancé et que Siger t'a donné une réponse fausse, je te donne la bonne équation pour (m):

Essaie de la retrouver par toi-même puis de trouver l'équation de (m').

salut Romanouch,
La formule que j'ai utilisée : a=(yC-yB)/(xC-xB) est celle que j'ai appris pour calculer le coefficient directeur d'une droite ... du coup je l'ai appliqué pour essayer de calculer l'équation de la médiatrice (m).
Dans mes cours, en ce moment, on travaille sur l'orthogonalité (vecteur normaux, équations de cercle) et j'ai la formule "deux vecteurs u(x;y) et v(x';y') sont orthogonaux si et seulement si xx'+yy'=0" de par cette équation, on peut en déduire que le produit scalaire u.v est nul et le vecteur u (ou la droite dirigée par ce vecteur u) est perpendiculaire au vecteur v (ou à la droite dirigée par ce vecteur v) ...
Ensuite, j'ai essayer de retrouver l'équation de (m) mais je ne retombe pas sur vos pattes, je trouver toujours y=1/3x+3 et pour (m') je trouve y=-1.5x+3 :/

[coralyne]

Oui : 1/(1/3)=3 et ton équation :qui se simplifie en y=-3x+8 était tout à fait correcte. Après, si ton -2.7 lu sur le dessin correspond à la pente de la médiatrice de [BC], tu n'est pas si loin du compte que ça vu que par le calcul tu as trouvé un coefficient directeur de -3 (c'est vrai que ça fait quand même une erreur "non négligeable" de 3mm...)

Sinon, concernant l'équation (x-xB)²+(y-yB)²=(x-xC)²+(y-yC)², le x et le y, ben tu les garde "tels quels" : c'est exactement la même chose que quand tu écrit que l'équation d'une droite est (par exemple) y=3x+5 : x et y tu ne sait pas du tout combien il valent. Par contre, si on te donne les coordonnées x et y d'un point M, ça te permet immédiatement par un simple calcul de savoir si M est ou pas sur la droite.
Ben là, c'est pareil : on sait qu'un point M de coordonnées x et y est sur la médiatrice de BC] lorsque (x-xB)²+(y-yB)²=(x-xC)²+(y-yC)².
On pourrait effectivement directement remplacer (par exemple) x par 3 et y par 7 puis regarder si c'est vrai ou pas pour savoir si le point de coordonnées (3,7) est ou pas sur la médiatrice, mais il est bien plus malin de simplifier l'expression le plus possible en gardant les lettres x et y pour ensuite pouvoir vérifier bien plus rapidement si des points sont ou pas sur la médiatrice.

Ici, ça aurait donné
(x-0)^2+(y-3)^2=(x-3)²+(y-4)²
x²+y²-6y+9=x²-6x+9+y²-8y+16
8y-6y=-6x+16
y=-3x+8
et, heureusement, on trouve le même résultat qu'avec l'autre méthode.

Mais je le REDIT, ça semble être une autre méthode que celle attendu (l'intérêt, c'est qu'on peut l'appliquer même si on a "oublié" le calcul du coeff directeur d'une droite orthogonale à une droite donnée)

D'accord ok merci beaucoup !,
et donc ensuite, il faut que je calcule l'équation de (m') que je vérifie avec votre formule et que j'en déduise les coordonnées du centre du cercle circonscrit par un système d'équation à 2 inconnues ...
c'est ça !?

[Ben314]

D'un coté, si tu comprend parfaitement bien d'où "sort" l'équation de départ que je t'ai donné, c'est à dire (x-xB)²+(y-yB)²=(x-xC)²+(y-yC)² (voit tu bien le lien avec la notion de "médiatrice" ?), pourqui pas.

Mais le problème et Romanouch a tout à fait raison d'insister là dessus, c'est que si tu est sur la leçon sur le produit scalaire, je pense que ce n'est pas cette méthode qui est attendue, mais je ne connais pas le contenu des programmes de première :
1) As tu vu les équation de droite sous la forme ax+by+c=0 ?
2) La notion de "vecteur normal" à la droite ?
3) La notion de "vecteur directeur" de la droite ?
4) Le lien entre les points 1) à 3) ?

@Romanouch et siger et ou... autres : Je pense pas qu'ils "balancent" comme ça le fait qu'une droite orthogonale à une droite de pente p a elle même pour pente -1/p. Tu sais comment c'est présenté en première ?

[Romanouch]

salut Romanouch,
La formule que j'ai utilisée : a=(yC-yB)/(xC-xB) est celle que j'ai appris pour calculer le coefficient directeur d'une droite ... du coup je l'ai appliqué pour essayer de calculer l'équation de la médiatrice (m).
Dans mes cours, en ce moment, on travaille sur l'orthogonalité (vecteur normaux, équations de cercle) et j'ai la formule "deux vecteurs u(x;y) et v(x';y') sont orthogonaux si et seulement si xx'+yy'=0" de par cette équation, on peut en déduire que le produit scalaire u.v est nul et le vecteur u (ou la droite dirigée par ce vecteur u) est perpendiculaire au vecteur v (ou à la droite dirigée par ce vecteur v) ...
Ensuite, j'ai essayer de retrouver l'équation de (m) mais je ne retombe pas sur vos pattes, je trouver toujours y=1/3x+3 et pour (m') je trouve y=-1.5x+3 :/

Salut,

Si tu veux calculer le coefficient directeur d'une droite passant par les points B et C, alors effectivement ta formule fonctionne.

Mais calculer le coefficient directeur de la droite (m) n'est pas la même chose. D'abord, (m) ne passe ni par B ni par C, puisque c'est la médiatrice du segment [BC].
Deuxièmement, tu ne connais qu'un seul point par lequel passe (m): le point N. Il t'en faudra un autre pour pouvoir utiliser cette formule.
Cette formule ne semble donc pas être celle qu'il faille utiliser.

Si vous êtes en train d'étudier les vecteurs directeurs de droites, la perpendicularité et le produit scalaire, vous avez peut-être déjà fait un exercice consistant à déterminer l'équation d'une droite perpendiculaire à une autre droite dont on connaît l'équation. Regarde si tu retrouves ça, ça t'aidera.

Il existe des tonnes de méthodes pour résoudre ce problème, je pense que la meilleure, c'est d'utiliser celle que tu étudies en ce moment, car c'est par les exercices qu'on comprend ce qu'on étudie en maths (généralement).

Ps. j'en profite pour faire une petite remarque. La formule a=(yC-yB)/(xC-xB) que tu as utilisée est très efficace mais en 1eS il faut que tu comprennes d'où elle vient et comment tu peux la retrouver. Des formules, tu en auras tellement à apprendre durant ta scolarité que ton cerveau finira par exploser si tu essaies de tout retenir par coeur. L'avantage de cette façon de faire, c'est que, puisque tu comprends vraiment d'où vient la formule, tu l'utiliseras quand il faut.

[coralyne]

Ben314:
Je ne vois d'où "sort" votre équation de départ, je n'ai pas vu cette équation... Dans le chapitre que je suis en ce moment, il y a l'équation de cercle qui y ressemble, a par ça, je ne vois pas.
Ensuite, je ne suis plus sur le produit scalaire, on l'a vu en début d'année et dans le chapitre où je suis, il intervient, juste pour démontrer qu'un triangle est rectangle est en quel point or dans mon exercice, le triangle n'est pas rectangle...
Dans tout ce vous m'avez citer:
1) j'ai vu que toutes les droites admettent une équation de la forme ax+by+c=0;
2) la notion de vecteur normal, je sais que le vecteur u est perpendiculaire au vecteur v équivaut à : vecteur u"scalaire"v=0, pour démontrer qu'ils sont orthogonaux, qu'un vecteur normal à ine droite de vecteur directeur u est un vecteur non nul orthogonal au vecteur u et qu'un vecteur normal a pour coordonnées (a;b);
3) la notion de "vecteur directeur" d'une droite est lorsqu'un vecteur à la même direction que cette droite, et le vecteur directeur à pour coordonnées (-b;a)
4) enfin, le lien que j'en déduis entre le points 1 à 3 est qu'une droite, dirigée par un vecteur directeur u, admet un vecteur normal n(a;b) si et seulement si elle admet une équation cartésienne de la forme ax+by+c=0.

Romanouch:
C'est vrai que j'avais oublié que j'avais besoin de deux point appartenant à la droite pour calculer le coefficient directeur de cette droite x) .. du coup pour la droite (m), il faut que je fasse intervenir un point M(x;y) avec les coordonnées de N !? genre a=(yM-yN)/(XM-xN), qui serait égale à (y-3.5)/(x-1.5) mais sa mène à rien !?...
J'ai cherché dans mes cours et dans mes exos, je n'ai pas fait d'exos pour déterminer l'équation d'une droite perpendiculaire à une autre dont je connais l'équation ... le seul que j'ai fait était un exo de dm: l'énoncé donnait deux droites et les équations de chacune, il fallait trouver les vecteurs normaux de chacune et y'avait une question du genre "ces droites sont elles perpendiculaires?" et j'ai eu faux à la question là --'

[Romanouch]

Romanouch:
C'est vrai que j'avais oublié que j'avais besoin de deux point appartenant à la droite pour calculer le coefficient directeur de cette droite x) .. du coup pour la droite (m), il faut que je fasse intervenir un point M(x;y) avec les coordonnées de N !? genre a=(yM-yN)/(XM-xN), qui serait égale à (y-3.5)/(x-1.5) mais sa mène à rien !?...
J'ai cherché dans mes cours et dans mes exos, je n'ai pas fait d'exos pour déterminer l'équation d'une droite perpendiculaire à une autre dont je connais l'équation ... le seul que j'ai fait était un exo de dm: l'énoncé donnait deux droites et les équations de chacune, il fallait trouver les vecteurs normaux de chacune et y'avait une question du genre "ces droites sont elles perpendiculaires?" et j'ai eu faux à la question là --'

Ok, ça ne mène à rien de chercher un deuxième point, donc ce n'est pas la bonne piste effectivement.

Je te donne une piste sous la forme d'une question:
Si le vecteur u de coordonnées (a;b) est perpendiculaire au vecteur v de coordonnées (c;d), on peut déduire, comme tu l'as dis, que leur produit scalaire est nul, ce qui s'écrit: .
Quelle équation, avec les coordonnées des vecteurs, peut-on alors déduire?

[coralyne]

Ok, ça ne mène à rien de chercher un deuxième point, donc ce n'est pas la bonne piste effectivement.

Je te donne une piste sous la forme d'une question:
Si le vecteur u de coordonnées (a;b) est perpendiculaire au vecteur v de coordonnées (c;d), on peut déduire, comme tu l'as dis, que leur produit scalaire est nul, ce qui s'écrit: .
Quelle équation, avec les coordonnées des vecteurs, peut-on alors déduire?

on peut en déduire que ac+bd=0 !?

[coralyne]

Est-ce qu'un vecteur normal peux "couper" une droite ?
par exemple si je dis que le vecteur BC de coordonnées (3;1) est un vecteur normal de la droite (m) passant par le point N, milieu de [BC], c'est possible ?
ou je suis obliger de choisir le vecteur BN, de façon a ce que la droite ne soit pas "couper" ?

[Romanouch]

on peut en déduire que ac+bd=0 !?

Exact!

Maintenant, je découpe les étapes en question pour te guider plus. C'est une méthode pour trouver l'équation de (m), mais il y en a d'autres. Celle-là te permettra d'utiliser le produit scalaire et donc de mieux le maîtriser.

1. Quelles sont les coordonnées du vecteur ?
2. Nous allons noter l'équation de la droite (m) comme ceci: y=ax + b. Dans ce cas, quelles sont les coordonnées du vecteur directeur de (m)? On l'appelera
3. Que peut-on dire de et de ?
4. EN déduire le coefficient directeur de (m)
5. Le point N appartient à la droite (m). En déduire l'ordonnée à l'origine de la droite (m)
6. A ce stade, tu auras obtenu l'équation de (m)

Si tu y arrives et que tu retrouves la même équation que moi et que tu as compris, fais la même chose avec la droite (m'). Donne tes résultats au fur et à mesure si tu veux que je les valide ou si tu as des questions.