Equation: 1024=2^n ????

[Roxane38]

Bonjour! :we:
Est-il possible de résoudre l'équation 1024=2^n ????
C'est dans un exercice sur les suites. Et je bloque sur cette équation...
Merci à vous

[Euler911]

Bonjour,

[Euler911]

(méthode à utiliser: décomposition en facteurs premiers...);)

[Roxane38]

(méthode à utiliser: décomposition en facteurs premiers...);)

C'est à dire? :hein:

[Euler911]

Donc: 1024=2*2*2*2*2*2*2*2*2*2=2^10

[magnolia86]

(méthode à utiliser: décomposition en facteurs premiers...);)

...divisions par 2 en fait. :zen:

[Euler911]

2 est premier que je sache... :happy2:

[rene38]

Bonjour

Bonjour! :we:
Est-il possible de résoudre l'équation 1024=2^n ????
C'est dans un exercice sur les suites. Et je bloque sur cette équation...
Merci à vous
__________________
TermS

[magnolia86]

2 est premier que je sache... :happy2:

Certes, mais on ne se sert pas du tout de cette propriété de 2 : toi-même, tu as fait simplement des divisions, non ?

Même problèmes : résoudre (dans N) les équations 123456789 = 10^n ou 123456789 = 9^n
ça se fait par divisions successives par 10 (ça va aller vite !) ou 9... comme tu l'as fait avec 2 !

[Euler911]

Ok au temps pour moi;)

[Roxane38]

Très bien, merci à vous... :D
Je pensais qu'il y avait une méthode plus rapide mais non alors.
Je ne comprends pas la méthode de rene38, et je ne vais pas chercher à comprendre car elle ne parait pas à mon niveau...
Merci :)

[Billball]

Très bien, merci à vous...
Je pensais qu'il y avait une méthode plus rapide mais non alors.
Je ne comprends pas la méthode de rene38, et je ne vais pas chercher à comprendre car elle ne parait pas à mon niveau...
Merci

de méme (j'aimerais bien comprendre!) mais apparemment c'est utile et rapide!

[magnolia86]

rene38 expliquera surement mieux que moi ce qu'il a voulu dire.

Mais si je peux me permettre, rene38 a donné la manière classique de résoudre (en le réel ) l'équation avec deux réels positifs.
La solution est ( où 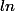désigne la fonction logarithme népérien)

C'est quelque chose à savoir (niveau TS), et les calculettes calculent très bien cette fonction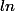 : si vous demandez à votre calculette combien vaut , elle va répondre 10 (ou 10.000000000001 ou 9.999999999999 par approximation).

Cela dit, à la main, impossible de calculer ln(1024) qui est réel, ln(2) aussi, etc.

[masiuxus]

Remarque en passant : en TS, on devrait savoir quand même calculer les puissances successives de 2, surtout qu'elles servent en informatique ...
2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 ... c'est pas très long de parvenir à 1024 ... Quant à l'unicité, comme dirait un prof de fac ... elle est triviale ! :ptdr:

[oscar]

Bonjour

Si je peux me permettre de compléter

n = ln 1024/ ln2
<=>

n = ln (2 ^10) / ln 2 ( formule ln A ^n = n log A)
or ln (2 ^10) = 10 ln 2

Donc n=...

[magnolia86]

Bonjour

Si je peux me permettre de compléter

n = ln 1024/ ln2


n = ln (2^10) / ln 2
or ln (2 ^10) = 10 ln 2

Donc n=...

ok, mais là on évoque la solution pour la retrouver, donc c'est tricher :we:

[oscar]

???

Je ne comprends pas votre réaction...

[Billball]

C'est quelque chose à savoir (niveau TS), et les calculettes calculent très bien cette fonction : si vous demandez à votre calculette combien vaut , elle va répondre 10 (ou 10.000000000001 ou 9.999999999999 par approximation).

merci *a pris note!*

[magnolia86]

???
Je ne comprends pas votre réaction...

Alors explication il doit y avoir :we:

On veut résoudre
Evidemment, on ne sait pas par coeur que , sinon on n'utilise pas le .
Bon il vient . Maintenant, dans cette expression, si on remplace 1024 par , c'est qu'on sait par coeur que et qu'on l'utilise... pour obtenir la solution à l'équation . C'est pas logique.

ok ?

[Euler911]

C'est bien d'utiliser les logarithme et exponentielle, mais lorsque l'on constate que 2|1024 ... autant utiliser quelque chose de moins lourd théoriquement... Surtout si par la suite on doit simplifier ln(1024)/ln(2)!!!!!!!

m'enfin, c'est mon avis.