On nous a demander de déterminer ces ensemble en extension
A={x appartient àZ/ (x^2-x+2)/2x+1 appartenient à Z}
Ensemble en extension
13 messages
- Page 1 sur 1
Re: Ensemble en extension
perso, je poserais bien k= 2x+1
on remplace, on arrive à
k impair et k-5/2+3/k entier relatif
soit
k impair et -5/2+3/k entier relatif
on remplace, on arrive à
k impair et k-5/2+3/k entier relatif
soit
k impair et -5/2+3/k entier relatif
Re: Ensemble en extension
Ok merci je vais essayer ceci
Mais juste une p'tit question d où t'as eu k-5/2+3
Mais juste une p'tit question d où t'as eu k-5/2+3
Re: Ensemble en extension
Salut,
<=> k entier impair et -5+6/k entier pair <=> k impair et 6/k entier impair
Mais bon, d'un autre coté, il faudrait savoir si dans la définition de A, c'est bien (x^2-x+2)/2x+1=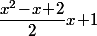 comme c'est écrit dans le premier post. ou si "par hasard", ça serait pas plutôt (x^2-x+2)/(2x)+1, voire même (x^2-x+2)/(2x+1)
comme c'est écrit dans le premier post. ou si "par hasard", ça serait pas plutôt (x^2-x+2)/(2x)+1, voire même (x^2-x+2)/(2x+1)
Eventuellement, on peut rajouter une petite ligne de plus :pascal16 a écrit:. . . <=> k entier impair et -5/2+3/k entier relatif
<=> k entier impair et -5+6/k entier pair <=> k impair et 6/k entier impair
Mais bon, d'un autre coté, il faudrait savoir si dans la définition de A, c'est bien (x^2-x+2)/2x+1=
Modifié en dernier par Ben314 le 15 Oct 2018, 13:20, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Ensemble en extension
il y a quelques jours, on a eut une autre façon de faire
(x^2-x+2)/2x+1 =n, n entier relatif
=> équation du seconde degré où racine de delta doit être un entier
(x^2-x+2)/2x+1 =n, n entier relatif
=> équation du seconde degré où racine de delta doit être un entier
Re: Ensemble en extension
De toute façon, il y a des tas de façon de faire.
Je pense que perso. je ferait plutôt comme dans ton premier post., à savoir une division polynomiale (plus ou moins "cachée" selon le public), vu que ça continuerais à marcher avec des truc de degré plus grand que 2, mais pourquoi pas utiliser l'exo. pour faire réviser les équations du second degré...
Je pense que perso. je ferait plutôt comme dans ton premier post., à savoir une division polynomiale (plus ou moins "cachée" selon le public), vu que ça continuerais à marcher avec des truc de degré plus grand que 2, mais pourquoi pas utiliser l'exo. pour faire réviser les équations du second degré...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Ensemble en extension
pascal16 a écrit:il y a quelques jours, on a eut une autre façon de faire
(x^2-x+2)/2x+1 =n, n entier relatif
=> équation du seconde degré où racine de delta doit être un entier
le quotient est mal parenthésé.
Re: Ensemble en extension
Bonjour;
Soient x et n tels que (x;n) un élément de IR x Z .
Supposons qu'on a : (x² - x + 2)/(2x + 1) = n ; donc : x² - (2n + 1)x - (n - 2) = 0 ;
donc : Delta = 4(n + 1)² - 11 = s² ; avec s un élément de IR ;
donc : (2n +2 - s)(2n + 2 + s) = 11 ;
donc : (n = 2 et s = 5) ou (n = 2 et s = - 5) ou (n = - 4 et s = 5) ou (n = - 4 et s = 5);
donc : si (n = 2 et s = 5) ou (n = 2 et s = - 5) on a x1 = 0 et x2 = 5 ;
et si (n = - 4 et s = 5) ou (n = - 4 et s = - 5) x3 = - 1 et x2 = - 6 ;
donc : A = {- 6 ; - 1 ; 0 ; 5} .
PS : Suite à la remarque de Pascal , j'ai corrigé mes erreurs : x est un nombre entier relatif,
donc : (2n + 1 +/- s)/2 l'est aussi ; donc s est aussi un nombre entier relatif .
Soient x et n tels que (x;n) un élément de IR x Z .
Supposons qu'on a : (x² - x + 2)/(2x + 1) = n ; donc : x² - (2n + 1)x - (n - 2) = 0 ;
donc : Delta = 4(n + 1)² - 11 = s² ; avec s un élément de IR ;
donc : (2n +2 - s)(2n + 2 + s) = 11 ;
donc : (n = 2 et s = 5) ou (n = 2 et s = - 5) ou (n = - 4 et s = 5) ou (n = - 4 et s = 5);
donc : si (n = 2 et s = 5) ou (n = 2 et s = - 5) on a x1 = 0 et x2 = 5 ;
et si (n = - 4 et s = 5) ou (n = - 4 et s = - 5) x3 = - 1 et x2 = - 6 ;
donc : A = {- 6 ; - 1 ; 0 ; 5} .
PS : Suite à la remarque de Pascal , j'ai corrigé mes erreurs : x est un nombre entier relatif,
donc : (2n + 1 +/- s)/2 l'est aussi ; donc s est aussi un nombre entier relatif .
Modifié en dernier par aymanemaysae le 16 Oct 2018, 09:58, modifié 4 fois.
Re: Ensemble en extension
avec s un élément de IR : (2n +2 - s)(2n + 2 + s) = 11 ; donc : n = 2 et s = 5
(s²=25, s vaut +5 ou -5)
mais avec s dans R, comment justifier que ton produit est le produit de deux nombres entiers ?
essaie x=-6 ...
(s²=25, s vaut +5 ou -5)
mais avec s dans R, comment justifier que ton produit est le produit de deux nombres entiers ?
essaie x=-6 ...
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 133 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
