Ensemble en extension

[Ilyaskilango]

Salut voilà un autre ensemble qu'il faut l'écrire en extension , je suis bloquer par où commencer et quel méthode faire
Voilà l'ensemble
B={x appartenant à Z / (x+1)/(2x-1) appartenient à Z}
Voilà c'est tt

[pascal16]

pour x >0, dès que x est un peu "grand", 0<(x+1)/(2x-1)<1, donc pas dans Z
(2x-1) est en plus un nombre impair

pour x >0
E((x+1)/(2x-1) ) <1 pour quelles valeurs de x ?

même raisonnement pour pour x <0

il doit rester 4-5 cas proches de 0 à gérer à la main

[Ben314]

Ben ça correspond à chercher les dans 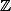tels que .
Y'a des tas de méthodes possible, par exemple étudier les variation de la fonction (de R dans R) .
Après, si on veut être "un peu astucieux", on peut aussi écrire que ce qui signifie que doit être un entier impair (vu qu'il doit être égal à ) donc en particulier que l'entier doit être un diviseur de 3 ce qui laisse peu de possibilités.

[Ilyaskilango]

Donc les cas possible seront
3/(2x-1)=1 Et 3/(2x-1)=-1 et 3/(2x-1)=3 Et 3/(2x-1)=-3

Donc y'a que valeurs 1 Et 2 et -1 et 0
C'est tt ?

[Ben314]

Oui.
Et là, vu que l'ensemble est fini, tu peut effectivement le décrire en extension : B={-1;0;1;2}

[Ilyaskilango]

Oui merci beaucoup

[Ilyaskilango]

Stp juste une p'tit question si on vous dit de déterminer en extension
A union B avec A=[-2,1] Et B={-1;0;1;2}