Ensemble de droites

[Alex6589]

Bonjour, j'ai un autre exercice à faire que je ne comprend pas du tout.

Pour tout réel m , on appelé Dm l'ensemble des points M dont les coordonnées (x;y) vérifient :
(m+1)y-(m+2)x +1= 0

1- Déterminer et construire D2. Je suis bien consciente que vous ne pourrez pas me construire D2 mais seulement des conseils et des indications pour la construire m'aideront.

2- Démontrer que, quelle que soit la valeur de m, Dm est une droite du plan

3- Determiner les réels m pour lesquels la droite Dm est parallèle à l'un des axes de coordonnées
( ce n'est même pas que je n'ai pas réussi à faire cette question, c'est que je ne la comprend même pas !)

4- Montrer que toutes les droites Dm passent par un point À sont on donnera les coordonnées.

Merci par avance pour l'aide que vous m´apporterez

[aviateur]

Bjr
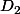tu remplaces donc m par 2. Pour tracer la droite tu cherches 2 points
Tu choisis par exemple x=0 et tu trouve une valeur de y. De même tu choisis un autre x=1 (ou 2 ou 5) et tu trouve un autre point.

Alors je viens de voir la question 2!! Alors là, c'est à la fois simple et compliqué. Parce que ce n'est pas une question qu'on pose si on a déjà étudié l'équation d'une droite car c'est évident. Cela sous-entend que ce n'est pas encore vu. Pour répondre cela donc de la construction de ton cours et ça je peux pas le savoir.

Les droites // à Ox ont pour équation y=cste
Les droites // à Oy ont pour équation x=cste à toi de voir pour quels m c'est le cas.

Soit A=(a,b) un point commun à toutes les droites D_m alors on a
(m+1)b-(m+2)a +1= 0

Soit m(b-a)+b-2 a +1 =0 pour tout m. Cherche pour quel couple (a,b) c'est possible

[Alex6589]

Merci beaucoup, jai déjà étudié l'équation de droite de type cartésienne ax +by +c = 0 mais je vois pas comment demontrer ce qui est posé en question 2 avec ca

[aviateur]

Disons que c'est une équation de droite ssi
Donc il faut simplement expliquer que c'est toujours vrai pour tout m.

[Alex6589]

Merci, jai répondu à la question 1. J'ai trouvé un point de la droite D2 qui a pour coordonnées (3;4) et un autre (6;8).

Mais pour la question 2 je ne comprend toujours pas quel calcul faire!

[triumph59]

Bonjour,

Pour la question 1)

D2 est l'ensemble des points M dont les coordonnées (x;y) vérifient : (2+1)y-(2+2)x +1= 0, soit 3y-4x+1=0

Si je prends le point A(3;4), j'obtiens

Je te laisse recalculer les coordonnées des 2 points car il y a une erreur dans ton calcul

[Alex6589]

Oui merci j'avais oublié le "+1" dans 3y -4x +1 .
Mais pour la question 2 je dois faire comment ?

[triumph59]

Question 1)
Peux-tu redonner 2 points que nous puissions vérifier que tu as trouvé la bonne réponse

Question 2)
Pour les équations de droite, on a plutôt l'habitude de les voir sous la forme y=ax+b ... essaie de mettre ton équation sous cette forme et tu verras qu'il y a un cas particulier à traiter à part et un cas général qui correspond à l'équation d'une droite

[Alex6589]

Pour la question 1 jai deux points de coordonnes (0;-1/3) et (1;1)

[Alex6589]

Pour ma construction jai plutôt choisi A(1;1) et B(7;9)

[Alex6589]

La question 2 je ne vais pas la faire car je comprend pas du tout. Cependant pour la question 3 j'ai trouvé : pour que D soit parallèle à l'axe des abscisses il faut que m = -2 et pour que D soit parallèle à l'axe des ordonnées il faut que m = -1
Est ce que c'est juste ?
Merci

[pascal16]

A(1;1) et B(7;9) -> ils sont bien sur D2
ok pour m=-1 et m=-2

[Alex6589]

Merci et donc pour la 4 pour trouver le couple (a;b) ou (x;y) je fais comment ?

[pascal16]

quand on a fait un peu de théorie de polynomes, c'est facile

sol 1 : on trace, on trouve le point puis on démontre que c'est lui

sol 2 : on est imaginatif

il faut x et y tels que pour toute valeur de m, on ait :
(m+1)y-(m+2)x +1= 0
met ça sous une forme où c'est m qui est en facteur (..?.) m +(..??.) =0
si c'est vrai pour m=0 , il faut (..??.)=0
et ensuite comme (..??.)=0, on a (..?.) m =0 pour toute valeur de m, en particulier quand m est non nul
soit (..?.) =0
il y a 1 seul couple (x;y) qui vérifie tout ça.

[Alex6589]

Merci beaucoup