Merci à tout ceux qui auront la gentillesse (et la patience) de m'aider et de m'expliquer ce petit exercice.
J'ai bien compris l'enoncé mais je sais pas comment y répondre, oublie de méthode je pense .
Donc voilà :
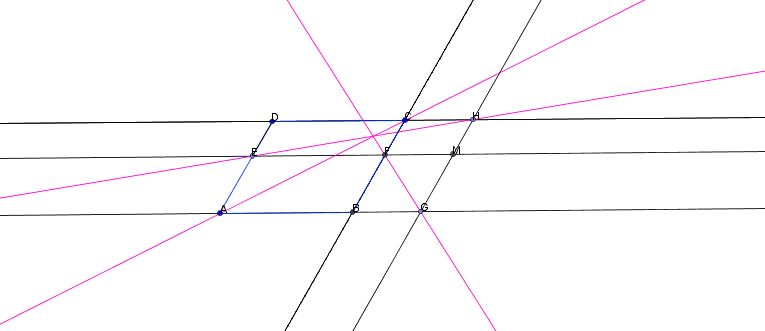
Soit ABCD un parrallélograme et un point M du plan. La parallèle à la droite (AB) passant par le point M coupe les droites (AD) et (BC) respectivement en E et F.
La parallèle à la droite (BC) passant par le point M coupe les droites (AB) et (CD) respectivement en G et H. Lorsque les points E,F, G et H sont distincts des sommets du parallélogramme ABCD, montrer que les doirtes (AC), (EH) et (FG) sont concourantes ou parrallèles.
Je pense qu'elles sont concourantes mais comment le montrer ?
Je pense qu'il faut :
se placer dans un repère (A,vectAB,vectAD)
On détermine les coordonnées des points A, B , C et D dans ce repère.
On pose ensuite M de coordonnées (x;y).
On détermine les coordonnées de E, F, G et H, puis les équations cartésiennes des droites (AC) (FG) et (EH).
On calcule les coordonnées de l'intersection de deux de ces droites et enfin on vérifie que ce point appartient à la troisième droite.
Mais je suis bloqué à l'avant dernière étape, je ne sais pas comment déterminer E, F, G et H.
Pouvez vous m'aider ? Merci beaucoup !