Divisibilité

[webnet]

Bonjour je n'arrive pas à commencer un exercice

determiner les entiers relatifs n tels que n-1 divise n+17

il faut donc trouver que n+17 = (n-1)*q avec q entier

mais aprés je ne sais pas continuer. Pouvez vous aussi m indiquer la bonne rédaction? merci!

[abcd22]

Bonsoir !
On peut remarquer que si n-1 divise n+17, alors n-1 divise aussi (n+17) - (n-1) = 18, on peut chercher si la réciproque est vraie.

[webnet]

Mais 18 ne fait pas partie des n qui vérifient ce que j ai mis dans l énoncé

[abcd22]

C'est n-1 divise 18 qu'on a obtenu comme condition nécessaire, attention à ne pas confondre n et n-1.

[BancH]

Il reste à montrer que :

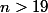
Si alors

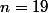
car pour on a:

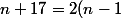[abcd22]

Ce n'est pas la peine de montrer que , c'est une conséquence de n-1 divise 18. Ce qui reste à montrer c'est que si n-1 divise 18 alors n-1 divise n+17 (et ne pas oublier qu'on a demandé les entiers relatifs et pas seulement les entiers positifs quand on donne l'ensemble des solutions).

[webnet]

OK donc si n-1=18 ou n-1= -18 mais aussi n-1 = 1 ou n-1 =-1
n prend comme valeurs -17, 0, 2,19

Arrivez vous à faire le même chose avec 5n+7 diviseur de 2n+16 ? la je ne sais pas...

[abcd22]

OK donc si n-1=18 ou n-1= -18 mais aussi n-1 = 1 ou n-1 =-1
n prend comme valeurs -17, 0, 2,19

Il te manque plein de diviseurs de 18 là (2, 3, 6, 9). La meilleure façon de rédiger la réciproque c'est de dire que si 18 = (n -1) k, où k est un entier relatif, alors n + 17 = n-1 + 18 = ... Si tu vérifies à la main pour chaque diviseur tu perds du temps.

[webnet]

Ok merci!

Au fait tu n as pas la solution pour 5n+7 diviseur de 2n+16 ???

[abcd22]

Arrivez vous à faire le même chose avec 5n+7 diviseur de 2n+16 ? la je ne sais pas...

C'est la même idée : on essaie de trouver une combinaison linéaire à coefficients entiers de (5n + 7) et (2n + 16) telle que les n disparaissent, pour trouver une condition de la forme « 5n + 7 divise "un nombre" ». Par contre là pour étudier la réciproque je pense qu'on est obligé de le faire à la main pour chaque diviseur possible du nombre qu'on trouve, à cause du 5 devant n : si on suppose 5n + 7 = 3 par exemple, on ne trouve pas un entier pour n (donc on n'aura pas l'équivalence entre « 5n + 7 divise 2n + 16 » et « 5n + 7 divise un nombre donné » cette fois).

[webnet]

Aprés avoir éffectué la combinaison je trouve 5n+7 divise 66,

donc 5n+6 divise tous les diviseurs de 66? donc 1,2,33. c'est tout?

[BancH]

Comme pour la question précédente tu n'as pas tous les diviseurs.

Et divise est faux.

[webnet]

Si tu parles des diviseurs négatifs il ne faut pas les prendre en compte!

Mais même en résolavnt avec ce que j ai les solutions ( n ) ne sont pas des eniers: ex 5n+7=66 n= 59/5 et ce n' est pâs bon!!!

[BancH]

Désolé j'ai effacé mon message... tu es sûr pour 66 ?

[BancH]

Au fait tu n as pas la solution pour 5n+7 diviseur de 2n+16 ???

Déjà faut voir que n ne peut pas être positif en essayant avec n=2 et n=1, et que la valeur absolue de n est proche de 0. Tu essaies avec quelques n: -4, -3, -2, -1 et tu as comme solutions -2 et -1.

Sinon je vois pas comment résoudre mathématiquement.

[webnet]

Donc d aprés ce que tu dis n est proche de 0 donc pas entier, donc il n y a aucune solution!

[webnet]

En plus dès le début on ne peut pas appliquer la combinaison linéaire, on a rien qui,divise à la fois 5+7 et n+16! non?

[rene38]

Bonjour

Bien confus, tout ça !
5+7 ? 5n+6 ? 5n+7 ?
n+16 ? 2n+16 ?
Si les 2 nombres sont ceux en gras, on trouve facilement n=-1 ou n=3

[BancH]

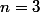
Oui c'est ce que j'ai dit , ou (lui je l'avais oublié).

Mais comment les trouver sans essayer de tête diffrérentes valeurs de ?

[webnet]

oui il faut trouver les n, entiers naturels tels que 5n+7 est un diviseur de 2n+16. Comment fais tu pour trouver?