En dehors de évident
Divisibilité
4 messages
- Page 1 sur 1
Divisibilité
Trouver tous les entiers positifs ) tels que
tels que  est divisible par
est divisible par  .
.
En dehors de évident=(a,a)) , j'ai trouvé quelques résultats par la force brute. Cependant, je n'ai aucune idée de comment construire une preuve rigoureuse. Votre aide sera appréciée!
, j'ai trouvé quelques résultats par la force brute. Cependant, je n'ai aucune idée de comment construire une preuve rigoureuse. Votre aide sera appréciée!
En dehors de évident
Salut,
J'ai une réponse, mais c'est assez "crado", mais, comme j'ai même pas peur du ridicule, je la donne quand même...
\ \Leftrightarrow\ <br />b^2+(1-k)ab+4(1-k)-ka^2=0\)
qui, vu comme une équation du second degré en , a pour discriminant :
, a pour discriminant :
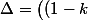a\big)^2-16(1-k)+4ka^2=(k^2-2k+1+4k)a^2+16(k-1)=\big((k+1)a\big)^2+16(k-1))
Or doit être le carré d'un entier qui doit être supérieur ou égal à
doit être le carré d'un entier qui doit être supérieur ou égal à a) et de même parité que
et de même parité que a) .
.
Ecrivons donc que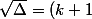a+2n\ (#)) où
où 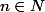 .
.
On a alorsa\pm\sqrt{\Delta}}{2}=ka+n) (car
(car 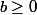 )
)
Reste à résoudre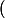) , c'est à dire
, c'est à dire a\big)^2+16(k-1)=\Big((k+1)a+2n\Big)^2) :
:
=4(k+1)an+4n^2\ \Leftrightarrow\ k(4-an)=4+an+n^2)
On doit donc avoir et cela ne fait pas "trés beaucoup" de cas à étudier.
et cela ne fait pas "trés beaucoup" de cas à étudier.
Aprés "essais", on trouve 4 solutions autres que celles où a=b (les solutions avec a=b correspond au cas où n=0)
EDIT : en reregardant la preuve, en fait l'équation de départ équivaut à(b+a)=4(k-1)) et je pense qu'avec ça, on peut résoudre même dans Z.
et je pense qu'avec ça, on peut résoudre même dans Z.
J'ai une réponse, mais c'est assez "crado", mais, comme j'ai même pas peur du ridicule, je la donne quand même...
qui, vu comme une équation du second degré en
Or
Ecrivons donc que
On a alors
Reste à résoudre
On doit donc avoir
Aprés "essais", on trouve 4 solutions autres que celles où a=b (les solutions avec a=b correspond au cas où n=0)
EDIT : en reregardant la preuve, en fait l'équation de départ équivaut à
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
