Divisibilité et Congruence.

[mat14men]

On considère la suite (Un) d'entiers naturels définie par:
U0=14
U n+1=5Un -6

1) calculer u1, u2, u3 et u4
Quelle conjecture pouvez vous émettre concernant les deux derniers chiffres de l'écriture de Un?

2) Démontrer que pour tout n entier naturel,
U n+2 est congrus à Un (mod4)
Déduisez que pour tout entier naturel k,
U 2k est congrus à 2 (mod 4)
et U 2k+1 est congrus à 0 (mod 4)

3) Démontrer par récurrence que, pour tout entier naturel n,
2 Un = 5^(n+2) +3

4) Déduire que, pour tout entier naturel n,
2 Un est congrus à 28 (mod 100)

5) Déterminer les deux derniers chiffres de l'écriture décimale de Un suivant les valeurs de n.
Soit d un diviseur commun à tous les un. Montrer que d=1 ou d=2.

Alors j'ai réussis la question 1), la question 2) aussi avec de la récurrence, la question 3) aussi, la question 4) avec de la récurrence également mais je bloque totalement sur la 5)... pourriez m'aider merci d'avance!

[Ben314]

Pour la première parti de la question 5), tu sait déjà que, pour tout entier n, ce qui signifie que (attention à diviser aussi le 100 : la première congruence dit que 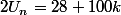et, si on divise tout par 2, ça fait )

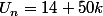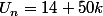Donc ou bien (dans la formule on considère les deux cas et )

Reste à savoir quels sont les n qui donne et lesquels donnent et c'est là qu'il faut utiliser les résultats de la question 2)

[capitaine nuggets]

On considère la suite (Un) d'entiers naturels définie par:
U0=14
U n+1=5Un -6

1) calculer u1, u2, u3 et u4
Quelle conjecture pouvez vous émettre concernant les deux derniers chiffres de l'écriture de Un?

2) Démontrer que pour tout n entier naturel,
U n+2 est congrus à Un (mod4)
Déduisez que pour tout entier naturel k,
U 2k est congrus à 2 (mod 4)
et U 2k+1 est congrus à 0 (mod 4)

3) Démontrer par récurrence que, pour tout entier naturel n,
2 Un = 5^(n+2) +3

4) Déduire que, pour tout entier naturel n,
2 Un est congrus à 28 (mod 100)

5) Déterminer les deux derniers chiffres de l'écriture décimale de Un suivant les valeurs de n.
Soit d un diviseur commun à tous les un. Montrer que d=1 ou d=2.

Alors j'ai réussis la question 1), la question 2) aussi avec de la récurrence, la question 3) aussi, la question 4) avec de la récurrence également mais je bloque totalement sur la 5)... pourriez m'aider merci d'avance!

Qu'as-tu trouvé déjà pour les questions précédentes ?

[mat14men]

Bah avec la congruence, j'ai démontrer ce qui était demandé..

[mat14men]

Pour la première parti de la question 5), tu sait déjà que, pour tout entier n, ce qui signifie que (attention à diviser aussi le 100 : la première congruence dit que et, si on divise tout par 2, ça fait )

Donc ou bien (dans la formule on considère les deux cas et )

Reste à savoir quels sont les n qui donne et lesquels donnent et c'est là qu'il faut utiliser les résultats de la question 2)

jusqu'à là, je comprend mais comment trouver les valeurs de n et la deuxième partie de la question?

[Ben314]

Vu que 4 divise 100, si tu sait à quoi est congru un nombre modulo 100, tu peut en déduire à quoi il est congru modulo 4. (car si x=y+100k alors x=y+4*(25k) )

Donc là, si Un est congru à 14 modulo 100, il est congru à quoi modulo 4 ?
Et s'il est congru à 64 modulo 100 ?

Au vu des résultat du 2) tu en déduit quoi ?

[mat14men]

Vu que 4 divise 100, si tu sait à quoi est congru un nombre modulo 100, tu peut en déduire à quoi il est congru modulo 4. (car si x=y+100k alors x=y+4*(25k) )

Donc là, si Un est congru à 14 modulo 100, il est congru à quoi modulo 4 ?
Et s'il est congru à 64 modulo 100 ?

Au vu des résultat du 2) tu en déduit quoi ?

Je suis vraiment perdu...
je ne vois pas le rapport avec ma récurrence de la question 2...
Cela fait quoi que un+2 congru à un modulo 4? et que u2k congru à 2 modulo 4? Je viens juste de commencer les congruences ducoup j'ai assez du mal à comprendre...

[Ben314]

Ici, ce n'est pa vraiment le problème de "comprendre les congruence", mais plutôt d'arriver à faire une synthèse de ce qui a été montré dans l'exercice :


Au 2) Tu as montré que lorsque n est pair et que lorsque n est impair.

Au 5) tu as montré que, pour n'importe quel n, on a ou bien (ce qui implique que ), ou bien (ce qui implique que )

Tu en déduit clairement (enfin il me semble...) qu'en fait quand n est pair et que quand n est impair.

[mat14men]

J'ai compris! C'est seulement de la logique enfaite! Merci!!!