Difficulté sur les limites de fontion
72 messages
- Page 1 sur 4 - 1, 2, 3, 4
difficulté sur les limites de fontion
Re bonjour a tous,
Me revoila avec un nouevau souci en maths, mais beaucoup plus dur :triste: .
Voici l'énoncé:
Soit f la fonction définie sur R par f(x) = x^3 + 4x² 4x + 1
1°) Déterminer la limite de f en ;). Préciser les opérations effectuées (par somme, par produit...).
Voila ma réponse
lim -x^3 = + l'infini
x-> -l'infini
lim +4x² = + l'infini
x-> -l'infini
lim -4x = + l'infini
x-> -l'infini
lim 1 = 1
x-> -l'infini
Donc par somme quand f(x) tend vers -l'infini x tend vers +l'infini.
Pour le moment tout va bien :happy3: , mais c'est apprès que c'est stressant :mur:
2°) a) Montrer que pour tout x > 0, f(x)= -x^3 (1-(4/x)+(4/x²)-(1/x^3)).
A noter que dans lénoncé il n'y a pas de parenthèse entre 4/x 4/x² et 1/x^3
Donc je vois bien qu'il y a un parallèle avec f(x) = x3 + 4x² 4x + 1, dans la grande parenthèse les exposants sont au dénominateur, mais là j'aoue je bloque totalement. Deja f(x) = x3 + 4x² 4x + 1, a été transformé en produit. alala enfin c'est la catastrophe :cry:
b) Déduire du 2°) a) la limite de f en +;). Préciser les opérations effectuées (par somme, par produit...).
bon là je vais savoir y faire avec l'opération de limite par produit.
Voili voilou.
Me revoila avec un nouevau souci en maths, mais beaucoup plus dur :triste: .
Voici l'énoncé:
Soit f la fonction définie sur R par f(x) = x^3 + 4x² 4x + 1
1°) Déterminer la limite de f en ;). Préciser les opérations effectuées (par somme, par produit...).
Voila ma réponse
lim -x^3 = + l'infini
x-> -l'infini
lim +4x² = + l'infini
x-> -l'infini
lim -4x = + l'infini
x-> -l'infini
lim 1 = 1
x-> -l'infini
Donc par somme quand f(x) tend vers -l'infini x tend vers +l'infini.
Pour le moment tout va bien :happy3: , mais c'est apprès que c'est stressant :mur:
2°) a) Montrer que pour tout x > 0, f(x)= -x^3 (1-(4/x)+(4/x²)-(1/x^3)).
A noter que dans lénoncé il n'y a pas de parenthèse entre 4/x 4/x² et 1/x^3
Donc je vois bien qu'il y a un parallèle avec f(x) = x3 + 4x² 4x + 1, dans la grande parenthèse les exposants sont au dénominateur, mais là j'aoue je bloque totalement. Deja f(x) = x3 + 4x² 4x + 1, a été transformé en produit. alala enfin c'est la catastrophe :cry:
b) Déduire du 2°) a) la limite de f en +;). Préciser les opérations effectuées (par somme, par produit...).
bon là je vais savoir y faire avec l'opération de limite par produit.
Voili voilou.
Oh, et bien je viens de trouver une idée qui marche ^^. Mais je trouve cela plutot bisarre
J'ai simplifié des fractions
donc
-x^3+ (4x*x*x/x) - (4x*x*x/x*x)+1
ce qui fait que lorsque l'on simplifie ça fait
-x^3 + 4x²- 4x + 1
you hou, j'ai réussi!! Je vous remercie énormement, car sans vous je pense que j'aurai encore cogité de longues heures^^
J'ai simplifié des fractions
donc
-x^3+ (4x*x*x/x) - (4x*x*x/x*x)+1
ce qui fait que lorsque l'on simplifie ça fait
-x^3 + 4x²- 4x + 1
you hou, j'ai réussi!! Je vous remercie énormement, car sans vous je pense que j'aurai encore cogité de longues heures^^
pour les limites quand x tend vers +;). Tout d'abord on fait par somme (pour tout ce qu'il y a dans la parenthèse) donc
lim 1 = 1 lim -4/x = 0 lim 4/x² = 0 lim -1/x^3= 0
x-> +;) x-> +;) x-> +;) x-> +;)
Par somme (1- 4/x + 4/x² - 1/x^3) tend vers 1 en +;)
Ensuite, lim -x^3 = -;)
x-> +;)
Par conséquent, par produit, f(x)= -x^3 (1- 4/x + 4/x² - 1/x^3) tend vers -;) en +;)
J'avour qu je ne suis pas très sûre de mon résultat :s
lim 1 = 1 lim -4/x = 0 lim 4/x² = 0 lim -1/x^3= 0
x-> +;) x-> +;) x-> +;) x-> +;)
Par somme (1- 4/x + 4/x² - 1/x^3) tend vers 1 en +;)
Ensuite, lim -x^3 = -;)
x-> +;)
Par conséquent, par produit, f(x)= -x^3 (1- 4/x + 4/x² - 1/x^3) tend vers -;) en +;)
J'avour qu je ne suis pas très sûre de mon résultat :s
Salut !
Pour la 2°)a) il te suffit de factoriser par le terme de plus haut degré de , c'est-à-dire,
, c'est-à-dire,  sous réserve que
sous réserve que 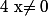 .
.
En ce qui concerne la 2°)b) c'est à priori une forme indéterminée :
Pour tout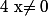 :
:
= -x^3 \( 1-\frac{4}{x}+\frac{4}{x^2}-\frac{1}{x^3} \))
Or


Donc=...)
et
Donc par conséquent,
On remarquera que) a la même limite que
a la même limite que 
----> On retiendra que la limite en ou
ou  d'une fonction polynôme est égale à la limite de son terme de plus haut degré.
d'une fonction polynôme est égale à la limite de son terme de plus haut degré.
En espérant t'avoir aidé :++:
Pour la 2°)a) il te suffit de factoriser par le terme de plus haut degré de
En ce qui concerne la 2°)b) c'est à priori une forme indéterminée :
Pour tout
Or
Donc
et
Donc par conséquent,
On remarquera que
----> On retiendra que la limite en
En espérant t'avoir aidé :++:
Lim -4/x= 0
x-> +;)
lim 4/x² =0
x-> +;)
lim -1/x^3= 0
x-> +;)
donc lim (1- 4/x+4/x²-1/x^3)= 0
x->+;)
et lim -x^3 = -;)
x-> +;)
Donc tu as bien raison c'est une forme indéterminée :'(. Cependant, on ne peut pas mettre la limite de 1? Comme ça on peut dire qu'il tend vers 1 et donc par produit ça fait - l'infini quand f(x) tend vers + l'infini. hihi
Si je fais tout ce meli melo, c'est parceque en cours nous n'avions pas eu le temps de bien travailler sur les limites, du coup mon cours se résume qu'à un tableau où il y a par exemple si on trouve +;) et -;) ( dans le cas de la somme) c'est une forme indéterminée. Mais ensuite on a rien pour plus approfondir l'étude :S.
C'est complexe^^. Mais bon je te remercie beacuoup Dinozzo13, j'ai tout compris dans tes explications.
x-> +;)
lim 4/x² =0
x-> +;)
lim -1/x^3= 0
x-> +;)
donc lim (1- 4/x+4/x²-1/x^3)= 0
x->+;)
et lim -x^3 = -;)
x-> +;)
Donc tu as bien raison c'est une forme indéterminée :'(. Cependant, on ne peut pas mettre la limite de 1? Comme ça on peut dire qu'il tend vers 1 et donc par produit ça fait - l'infini quand f(x) tend vers + l'infini. hihi
Si je fais tout ce meli melo, c'est parceque en cours nous n'avions pas eu le temps de bien travailler sur les limites, du coup mon cours se résume qu'à un tableau où il y a par exemple si on trouve +;) et -;) ( dans le cas de la somme) c'est une forme indéterminée. Mais ensuite on a rien pour plus approfondir l'étude :S.
C'est complexe^^. Mais bon je te remercie beacuoup Dinozzo13, j'ai tout compris dans tes explications.
Salut !
De rien ^^, c'est vrai qu'il n'est pas facile pour tout le monde de comprendre ça du premier coup, mais en persévérant, on peux y arriver :++:
Tiens, voici l'exercice comme promis.
Il traite des limites de fonctions, ses variations, dérivée, asymptotes et d'équations de tangente.
Onconsidère la fonction définie sur
définie sur  par :
par :
=\frac{-x^3+5x^2-7x+3}{(x-2)^2})
On note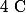 la représentation graphique de
la représentation graphique de  dans un repère orthonormal
dans un repère orthonormal ) (unité graphique : 2 cm).
(unité graphique : 2 cm).
1°)a) Calculer les limites de en
en  et en
et en  .
.
b) Calculer la limite de en
en  et interpréter le résultat.
et interpréter le résultat.
2°) Calculer) et vérifier que, pour tout
et vérifier que, pour tout  de
de  :
:
=\frac{(x-1)(-x^2+5x-8)}{(x-2)^3})
En déduire le sens de variations de et dresser son tableau de variations.
et dresser son tableau de variations.
3°) Montrer que, pour tout de
de  :
:
=-x+1+\frac{x-1}{(x-2)^2})
En déduire que la droite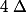 d'équation
d'équation  est asymptote à
est asymptote à  et étudier la position de
et étudier la position de  par rapport à
par rapport à  .
.
4°) Démontrer qu'il existe une droite tangente à
tangente à  et parallèle à
et parallèle à  ; donner une équation de
; donner une équation de  .
.
5°) Ecrire une équation de la droite tangente à
tangente à  au point d'abscisse 3.
au point d'abscisse 3.
6°) Tracer et
et  dans le repère
dans le repère ) ;
;
7°) Déterminer graphiquement, suivant les valeurs de m, le nombre de solutions de l'équation :
x^2+(4m-7)x+3-4m=0) .
.
Voilà, bonne révision, je serai là en cas de besoin ^^
De rien ^^, c'est vrai qu'il n'est pas facile pour tout le monde de comprendre ça du premier coup, mais en persévérant, on peux y arriver :++:
Tiens, voici l'exercice comme promis.
Il traite des limites de fonctions, ses variations, dérivée, asymptotes et d'équations de tangente.
Onconsidère la fonction
On note
1°)a) Calculer les limites de
b) Calculer la limite de
2°) Calculer
En déduire le sens de variations de
3°) Montrer que, pour tout
En déduire que la droite
4°) Démontrer qu'il existe une droite
5°) Ecrire une équation de la droite
6°) Tracer
7°) Déterminer graphiquement, suivant les valeurs de m, le nombre de solutions de l'équation :
Voilà, bonne révision, je serai là en cas de besoin ^^
Krapoplate a écrit:Lim -4/x= 0
x-> +;)
lim 4/x² =0
x-> +;)
lim -1/x^3= 0
x-> +;)
donc lim (1- 4/x+4/x²-1/x^3)= 0 [COLOR=Red]non ça fait 1
x->+;)
[/COLOR]
et lim -x^3 = -;)
x-> +;)
Donc tu as bien raison c'est une forme indéterminée :'(. Cependant, on ne peut pas mettre la limite de 1? Comme ça on peut dire qu'il tend vers 1 et donc par produit ça fait - l'infini quand f(x) tend vers + l'infini. hihi
ben si, c'est ce qu'il faut faire
Si je fais tout ce meli melo, c'est parceque en cours nous n'avions pas eu le temps de bien travailler sur les limites, du coup mon cours se résume qu'à un tableau où il y a par exemple si on trouve +;) et -;) ( dans le cas de la somme) c'est une forme indéterminée. Mais ensuite on a rien pour plus approfondir l'étude :S.
C'est complexe^^. Mais bon je te remercie beacuoup Dinozzo13, j'ai tout compris dans tes explications.
.....................
Bonjour. J'ai commencé l'exercice.
Pour le 1°aet b va bien. Mais pour le 2° c'est un peu plus dure.
Donc j'ai calculer f '. J'ai trouvé f'(x)= -3x²+10x-7/ (x-2)² . Mais voila où est le problème. J'ai developpé l'expression suivante, mais impossible de retrouver mon résultat :s. D'ailleur je ne comprend pas pourquoi il y a l'exposant cube au dénominateur, alors que dans l'expression f' que j'ai trouvé il y a un carré.
Pour le 1°aet b va bien. Mais pour le 2° c'est un peu plus dure.
Donc j'ai calculer f '. J'ai trouvé f'(x)= -3x²+10x-7/ (x-2)² . Mais voila où est le problème. J'ai developpé l'expression suivante, mais impossible de retrouver mon résultat :s. D'ailleur je ne comprend pas pourquoi il y a l'exposant cube au dénominateur, alors que dans l'expression f' que j'ai trouvé il y a un carré.
u'(x)= -3x²+10x-7
v' (x) = je n'arrive pas avec une expression entre parenthèse et au carré, mais si ma logique est bonne ça devrait faire 1. bon je t'expliques comment j'ai fait d'abord pour me simplifier les choses j'ai écrit de cette manière (x-2) (x-2). Ensuite, j'ai dérivé ces deux-ci donc (1)(1) ce qui donne 1. (J'ai l'impression que ce que je viens de donner comme réponse est désespérante :s)
v' (x) = je n'arrive pas avec une expression entre parenthèse et au carré, mais si ma logique est bonne ça devrait faire 1. bon je t'expliques comment j'ai fait d'abord pour me simplifier les choses j'ai écrit de cette manière (x-2) (x-2). Ensuite, j'ai dérivé ces deux-ci donc (1)(1) ce qui donne 1. (J'ai l'impression que ce que je viens de donner comme réponse est désespérante :s)
72 messages
- Page 1 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
