Salut,
Il me semble que c'est flou dans ta tête. Je vais donc reformuler entièrement cette preuve à ma manière, dans l'espoir que tu comprennes mieux.
Voici les 4 outils de la preuve. Si tu ne comprends pas un seul de ces points tu ne peux pas comprendre la preuve. Il faut donc bien comprendre chaque point suivant:
Rappel 1: Pour montrer qu'une fonction f est croissante sur un intervalle I, il faut montrer que si on a deux nombres m et n choisis dans l'intervalle I tels que m < n, alors f(m) < f(n). Ceci est la définition d'une fonction croissante.
Rappel 2: Pour montrer qu'une fonction f est décroissante sur un intervalle J, il faut montrer que si p et q sont deux nombres de l'intervalle J rangés tels que p < q, alors f(p) > f(q). Fais un dessin c'est très simple.
Rappel 3: Pour montrer qu'un certain nombre X est plus grand qu'un nombre Y, on peut étudier le signe du nombre X - Y. Si X - Y > 0, alors X>Y. Si X - Y < 0 alors X < Y
Rappel 4: Pour étudier le signe d'une expression produit par exemple \times (x + 20))
, on utilise un tableau de signes dans lequel on étudie le signe de chaque facteur (sais-tu le faire?)On considère la fonction
 = ax^2 + bx + c)
On suppose que a est un nombre positif dans toute cette preuve (on traitera le cas a négatif ensuite). Graphiquement, la parabole est tournée vers le haut et atteint son point le plus bas (minimum) en x = -b/2a
Objectif: On veut prouver que la fonction f est décroissante sur l'intervalle J =
On utilise donc le
rappel 2). On prend deux nombres p et q dans l'intervalle
rangés tels que
p < q. Notre objectif est donc de démontrer que
f(p) > f(q) Pour démontrer cela, on va
(rappel 3) étudier le signe du nombre
f(p) - f(q) = ap^2 + bp + c)
 = aq^2 + bq + c)
Donc:
 - f(q) = ap^2 + bp + c - (aq^2 + bq + c))
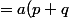(p - q) + b(p - q))
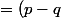[a(p + q) + b])
On doit étudier, je te le rappelle, le signe de
 - f(q) = (p - q)[a(p + q) + b])
On utilise le rappel 4): Pour étudier le signe du produit (p - q)[a(p+q) + b] on doit faire un tableau de signes avec (p - q) et (a(p+q) + b)
Quel est le signe de p - q? On sait que
p < q donc p - q est
toujours négatif
Quel est le signe de (a(p + q) + b) ? On sait que:
(car on l'a choisi comme ça !)
et aussi
DONC
En multipliant les deux membres par le nombre positif a (l'ordre ne change pas !) on trouve:
 < -b)
En ajoutant b aux deux membres, on trouve:
 + b < 0)
Donc le signe de a(p + q) + b est toujours négatif sur cet intervalle !
Conclusion: f(p) - f(q) est le produit de deux nombres négatifs (qui sont (p - q) et (a(p+q) + b)).
Donc f(p) - f(q) est un nombre positif
Donc f(p) - f(q) > 0 donc f(p) > f(q) et par le rappel 2 la fonction f est décroissante sur cet intervalle.Ensuite dans ta preuve, ils refont exactement le même raisonnement sur l'autre intervalle [-b/2a ; + infini[ en prenant deux nombres m et n de cet intervalle, en calculant f(m) et f(n), en faisant ensuite f(m) - f(n) pour prouver que f(m) < f(n)
par yann06 » 29 Déc 2016, 23:06
