Diamètre d' un graphe
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
kadaid
- Membre Relatif
- Messages: 257
- Enregistré le: 21 Nov 2011, 15:34
-
 par kadaid » 02 Aoû 2018, 11:31
par kadaid » 02 Aoû 2018, 11:31
Bonjour
Je ne comprends pas comment déterminer le diamètre d'un graphe.
Sur le dessin ci-joint on donne 3 pour le diamètre (distance maximale entre deux points: les cornes)
Pour moi, plutôt c'est 4
Merci pour des explications.

-
kadaid
- Membre Relatif
- Messages: 257
- Enregistré le: 21 Nov 2011, 15:34
-
 par kadaid » 02 Aoû 2018, 11:38
par kadaid » 02 Aoû 2018, 11:38
Je le refais car l'image n'apparait pas!

-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 02 Aoû 2018, 11:55
par hdci » 02 Aoû 2018, 11:55
Pourquoi la distance entre les deux points "cornes" serait-elle 4 ?
La distance entre deux points est la mesure du plus petit parcourt entre ces deux points, et la mesure d'un parcourt, c'est le nombre de segments qu'il emprunte.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 02 Aoû 2018, 11:57
par hdci » 02 Aoû 2018, 11:57
Et pour compléter : le diamètre est la plus grande des distances, mais pas le plus grand des parcourt !
Si c'était le plus grand des parcourt, le diamètre serait infini ((puisque rien n'interdit de passer deux fois par le même point, on ferait une infinité d'aller-retour).
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 02 Aoû 2018, 13:41
par aymanemaysae » 02 Aoû 2018, 13:41
Bonjour ;
Je rectifie : "le plus grand élément de C" au lieu de "le plus grand de C" .
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 02 Aoû 2018, 13:47
par pascal16 » 02 Aoû 2018, 13:47
On pourrait définir :
_ un diamètre eulérien : le plus long de l'ensemble des chemins les plus courts entre deux sommets qui passe par tous les sommets (ici 4).
_ un diamètre hamiltonien : le plus long de l'ensemble des chemins les plus courts entre deux sommets qui passe par toutes les arêtes (ici 6)
-
kadaid
- Membre Relatif
- Messages: 257
- Enregistré le: 21 Nov 2011, 15:34
-
 par kadaid » 02 Aoû 2018, 14:58
par kadaid » 02 Aoû 2018, 14:58
Merci pour vos réponses!
J'ai compris.
On détermine la distance (chemin le plus court) entre deux points à chaque fois et puis le diamètre est la plus grande de ces distances .
-
aviateur
 par aviateur » 02 Aoû 2018, 19:16
par aviateur » 02 Aoû 2018, 19:16
Bonjour,
Avec cette définition du diamètre quel est alors le diamètre du graphe G de
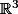
dont l'ensemble des sommets S est :
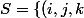\in R^3 : i,j,k \in [\![0,n ]\!])
,
)
et l'ensemble des côtés est constitué des segments
qui relient un sommet aux sommets les plus proches (au sens de la distance euclidienne)?
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 02 Aoû 2018, 19:57
par pascal16 » 02 Aoû 2018, 19:57
majorant : 3n
-
aviateur
 par aviateur » 02 Aoû 2018, 21:46
par aviateur » 02 Aoû 2018, 21:46
Bonjour
Je crois même que c'est 3n
-
aviateur
 par aviateur » 02 Aoû 2018, 21:55
par aviateur » 02 Aoû 2018, 21:55
Je me demande si on ne peut pas compliquer les choses, comme par exemple: soit dans
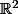
le graphe G dont l'ensemble S des sommets sont de coordonnées entières et sont situés à l'intérieur de l'ellipse d' équation

Deux sommets qcq sont reliés par un côté. Quel est le diamètre de G?
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 03 Aoû 2018, 09:57
par pascal16 » 03 Aoû 2018, 09:57
2 * max(E(a);E(b)) ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités

