Déterminer l'équation d'une parabole par rapport à sa représentation graphique

[Beatles]

Bonjour,

Je n'arrive pas à définir l'équation d'une parabole par rapport à sa représentation graphique.
Le but de l'exercice étant de trouver quelle est la hauteur maximale soit Bêta.
Pour cela si je ne me trompe pas il faut calculer Bêta= f(alpha).
Mais je ne comprend pas comment trouver alpha si je n'arrive pas à définir l'équation a(x-alpha)+Bêta

Je vous remercie d'avance pour votre aide.

[XENSECP]

Mouais c'est incomplet comme question/énoncé... Enfin je vois pas trop ce que tu attends de nous ;)

[SaintAmand]

Bonjour,

Je n'arrive pas à définir l'équation d'une parabole par rapport à sa représentation graphique.
Le but de l'exercice étant de trouver quelle est la hauteur maximale soit Bêta.

alpha est l'abscisse de l'extremum. Je ne suis pas sûr d'avoir compris votre problème.

[Adoration_For_None]

Bonjour,

Pour trouver graphiquement l'équation d'une parabole, il suffit de poser que est la représentation graphique d'une fonction f de la forme . Ensuite, sur ton graphique tu lis les solutions de (il en existe deux au maximum). De là tu déduis une factorisation de f qui est où et sont les solutions de . Ensuite tu développes ta factorisation comme ceci : . Et à partir de là, il suffit de prendre une abscisse k de la courbe qui a une image facile à lire, on connait ainsi . Donc nous pouvons résoudre (où y et k sont connus et a est l'inconnue). Une fois que tu as a tu n'as plus qu'à le replacer dans l'expression .

Bon un petit exemple pour éclaircir mes propos un peu théorique :



Première Étape : est la représentation graphique d'une fonction f de type .
Deuxième Étape : D'après le graphique, l'équation a deux solutions : 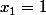et .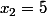
Troisième Étape : On peut ainsi déduire une factorisation de f, .
Quatrième Étape : On développe notre factorisation :
Cinquième Étape : Sur le graphique on lit aisément que . Ainsi .
Sixième Étape : On résous l'équation ainsi obtenu :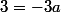 (je n'ai fais que calculer ce que j'avais dans la parenthèse et remplacer par sa valeur).
De là on déduit .
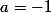Septième Étape : Nous pouvons ainsi conclure que
Étape Facultative : On développe l'expression obtenue pour l'avoir sous la forme .
On obtient ici : .

Voilà en espérant avoir été assez clair.

[Beatles]

Excusez moi c'est vrai que mon explication n'était pas très claire.

Voici l'énoncé:

Un joueur de football situé à 25m du but tente un tir et parvient à marquer.
Son ballon a franchi la ligne de but à une hauteur de 2,20 m, passant ainsi tout près de la barre transversale, puis a ensuite atteint le sol à 1m derrière la ligne de but.
Sachant que la trajectoire du ballon est une parabole, quelle hauteur maximale le ballon a-t-il atteinte ?

Il faut donc trouver la hauteur maximale de l'équation de la parabole soit Bêta= F(alpha).

[Beatles]

Bonjour,

Pour trouver graphiquement l'équation d'une parabole, il suffit de poser que est la représentation graphique d'une fonction f de la forme . Ensuite, sur ton graphique tu lis les solutions de (il en existe deux au maximum). De là tu déduis une factorisation de f qui est où et sont les solutions de . Ensuite tu développes ta factorisation comme ceci : . Et à partir de là, il suffit de prendre une abscisse k de la courbe qui a une image facile à lire, on connait ainsi . Donc nous pouvons résoudre (où y et k sont connus et a est l'inconnue). Une fois que tu as a tu n'as plus qu'à le replacer dans l'expression .

Bon un petit exemple pour éclaircir mes propos un peu théorique :



Première Étape : est la représentation graphique d'une fonction f de type .
Deuxième Étape : D'après le graphique, l'équation a deux solutions : et .
Troisième Étape : On peut ainsi déduire une factorisation de f, .
Quatrième Étape : On développe notre factorisation :
Cinquième Étape : Sur le graphique on lit aisément que . Ainsi .
Sixième Étape : On résous l'équation ainsi obtenu : (je n'ai fais que calculer ce que j'avais dans la parenthèse et remplacer par sa valeur).
De là on déduit .
Septième Étape : Nous pouvons ainsi conclure que
Étape Facultative : On développe l'expression obtenue pour l'avoir sous la forme .
On obtient ici : .

Voilà en espérant avoir été assez clair.

Merci pour ta réponse. Mais le problème est que je n'ai pas de graphique numéroté, j'ai juste un dessin avec des distanceS. En faite, c'est le dessin de la trajectoire d'un ballon: Un joueur de football situé à 25m du but tente un tir et parvient à marquer.
Son ballon a franchi la ligne de but à une hauteur de 2,20 m, passant ainsi tout près de la barre transversale, puis a ensuite atteint le sol à 1m derrière la ligne de but. La trajectoire du ballon est une parabole.
Je ne sais pas comment ajouter une photo, quelqu'un peut-il m'expliquer. Se serait peut-être plus simple...

[SaintAmand]

Le mouvement du ballon se fait dans un plan que vous pouvez munir d'un repêre orthonormé. L'énoncé vous fournit 3 points avec leurs coordonnées qui vont vous permettre de déterminer l'équation de la parabole en résolvant un petit système de 3 équations d'inconnues les coéfficients du polynôme.

[Beatles]

Bonjour,

Pour trouver graphiquement l'équation d'une parabole, il suffit de poser que est la représentation graphique d'une fonction f de la forme . Ensuite, sur ton graphique tu lis les solutions de (il en existe deux au maximum). De là tu déduis une factorisation de f qui est où et sont les solutions de . Ensuite tu développes ta factorisation comme ceci : . Et à partir de là, il suffit de prendre une abscisse k de la courbe qui a une image facile à lire, on connait ainsi . Donc nous pouvons résoudre (où y et k sont connus et a est l'inconnue). Une fois que tu as a tu n'as plus qu'à le replacer dans l'expression .

Bon un petit exemple pour éclaircir mes propos un peu théorique :



Première Étape : est la représentation graphique d'une fonction f de type .
Deuxième Étape : D'après le graphique, l'équation a deux solutions : et .
Troisième Étape : On peut ainsi déduire une factorisation de f, .
Quatrième Étape : On développe notre factorisation :
Cinquième Étape : Sur le graphique on lit aisément que . Ainsi .
Sixième Étape : On résous l'équation ainsi obtenu : (je n'ai fais que calculer ce que j'avais dans la parenthèse et remplacer par sa valeur).
De là on déduit .
Septième Étape : Nous pouvons ainsi conclure que
Étape Facultative : On développe l'expression obtenue pour l'avoir sous la forme .
On obtient ici : .

Voilà en espérant avoir été assez clair.

Le mouvement du ballon se fait dans un plan que vous pouvez munir d'un repêre orthonormé. L'énoncé vous fournit 3 points avec leurs coordonnées qui vont vous permettre de déterminer l'équation de la parabole en résolvant un petit système de 3 équations d'inconnues les coéfficients du polynôme.

Je vais essayer de faire vos méthodes. Merci.