Déterminant et inverse d'une matrice

[pascal16]

Tu veux faire deux choses à la fois.

Soit tu calcules l'inverse de la matrice :
si AX=B alors

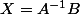
X=
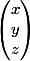
et B=

Soit tu fais un 'pivot de Gauss' ou de la substitition

[pascal16]

[Ben314]

Il me semble que s'il y a un problème entre ce qu'a écrit Pascal et ce que tu as fait, ça vient principalement du fait que :
- Dans ton premier post, la deuxième équation est 2x+2y+z=y' (et c'est ça qu'à résolu Pascal)
- Alors que sur ta feuille, c'est écrit petit, mais il me semble que dans la marge du haut, la deuxième équation est 2x+2y-z=y'