Donc là où je bloque, c'est sur le point numéro 3, le seul truc que j'ai compris, c'est que la droite passe par R :we: . Est-ce que vous auriez un chemin à m'indiquer pour que j'y comprenne quelque chose ? J'imagine qu'il y a un rapport entre coefficient directeur et coordonnées de droite, mais j'ai vraiment du mal à m'orienter :help: . Merci d'avance
Dérivées - tangente
3 messages
- Page 1 sur 1
Dérivées - tangente
Bonjour, je sollicite votre aide car je suis complètement perdu non pas sur un exercice, mais carrément sur sa correction :mur: . Je vous file le lien du pdf de l'excellent site xmaths.free.fr : Correction de l'exercice .
Donc là où je bloque, c'est sur le point numéro 3, le seul truc que j'ai compris, c'est que la droite passe par R :we: . Est-ce que vous auriez un chemin à m'indiquer pour que j'y comprenne quelque chose ? J'imagine qu'il y a un rapport entre coefficient directeur et coordonnées de droite, mais j'ai vraiment du mal à m'orienter :help: . Merci d'avance .
.
Donc là où je bloque, c'est sur le point numéro 3, le seul truc que j'ai compris, c'est que la droite passe par R :we: . Est-ce que vous auriez un chemin à m'indiquer pour que j'y comprenne quelque chose ? J'imagine qu'il y a un rapport entre coefficient directeur et coordonnées de droite, mais j'ai vraiment du mal à m'orienter :help: . Merci d'avance
bonjour,
def: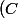) est la courbe ,
est la courbe ,  est la tangente,
est la tangente, la fonction.
la fonction.
Une tangente T à une courbe en , \qquad y_0=f(x_0))
est la droite qui passe par le point de la courbe
de la courbe
et, localement, colle "le mieux" à la courbe,
parmi toutes les droites sécantes en à la courbe.
à la courbe.
il y a deux façons de construire les droites tangentes:
En analyse en considérant le nombre dérivé de f
comme le coefficient directeur de cette droite tangente T
En algèbre, en considérant que le système, d'inconnue x,
=mx+p) admet, a priori, une racine double
admet, a priori, une racine double
égale à .
.
Car le point de contact ,entre la courbe C et la tangente T,
est limite des deux points d'intersection entre la courbe
et toute droite (non verticale) qui passe par M0.
on voit qu'en algèbre, nous avons à résoudre une équation
tandis qu'en analyse, il nous faut calculer une limite.
ici, pour la parabole, c'est le point de vue algébrique qui est retenu.
Evidemment, c'est un phénomène local (l'étude se fait à proximité de ,
,
et pour des polynômes de degré 3, la tangente peut bien recouper la courbe
ailleurs qu'en son point double en un point supplémentaire (inintéressant).
en un point supplémentaire (inintéressant).
def:
Une tangente T à une courbe en
est la droite qui passe par le point
et, localement, colle "le mieux" à la courbe,
parmi toutes les droites sécantes en
il y a deux façons de construire les droites tangentes:
En analyse en considérant le nombre dérivé de f
comme le coefficient directeur de cette droite tangente T
En algèbre, en considérant que le système, d'inconnue x,
égale à
Car le point de contact ,entre la courbe C et la tangente T,
est limite des deux points d'intersection entre la courbe
et toute droite (non verticale) qui passe par M0.
on voit qu'en algèbre, nous avons à résoudre une équation
tandis qu'en analyse, il nous faut calculer une limite.
ici, pour la parabole, c'est le point de vue algébrique qui est retenu.
Evidemment, c'est un phénomène local (l'étude se fait à proximité de
et pour des polynômes de degré 3, la tangente peut bien recouper la courbe
ailleurs qu'en son point double
mathelot a écrit:bonjour,
def:est la courbe ,
est la tangente,
la fonction.
Une tangente T à une courbe en
est la droite qui passe par le pointde la courbe
et, localement, colle "le mieux" à la courbe,
parmi toutes les droites sécantes enà la courbe.
il y a deux façons de construire les droites tangentes:
En analyse en considérant le nombre dérivé de f
comme le coefficient directeur de cette droite tangente T
En algèbre, en considérant que le système, d'inconnue x,admet, a priori, une racine double
égale à.
Car le point de contact ,entre la courbe C et la tangente T,
est limite des deux points d'intersection entre la courbe
et toute droite (non verticale) qui passe par M0.
on voit qu'en algèbre, nous avons à résoudre une équation
tandis qu'en analyse, il nous faut calculer une limite.
ici, pour la parabole, c'est le point de vue algébrique qui est retenu.
Evidemment, c'est un phénomène local (l'étude se fait à proximité de,
et pour des polynômes de degré 3, la tangente peut bien recouper la courbe
ailleurs qu'en son point doubleen un point supplémentaire (inintéressant).
J'en demandai pas tant :p. J'ai pu comprendre là où je bloquais ! Merci beaucoup l'ami
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
