Derivation fonction

[Tysse]

Bonjour !
J'ai un exercice à faire, je l'ai pratiquement fini seulement je bloque sur la deuxième partie de la question.

L'énoncé est : calculer les dérivées des fonctions suivantes en précisant leur domaine de dérivation.

1. F(X)= (sin(X)/cos(X)) définie sur ]-π/2;π/2[
2. G(X)= ✓4x-2 définie sur [1/2;+infini[.

Alors j'ai réussi à calculer les dérivées mais je ne sais pas ce qu'est le domaine de dérivation d'où je bloque sur comment il faut le préciser. Donc si quelqu'un pouvais m'aider se serait génial !
Merci d'avance pour vos réponse !

[Pisigma]

Bonjour,

Comment trouver le domaine de dérivabilité d'une fonction ?

Calculer l'ensemble de dérivation d'une fonction, généralement noté Df′, revient à calculer l'ensemble de définition de sa fonction dérivée. Regarder dans R=]−∞;+∞[, les valeurs pour lesquelles la fonction dérivée n'est pas définie. C'est à dire les valeurs de x telles que f′(x) n'existe pas.

Le calcul du domaine de dérivation est donc composé de 2 étapes :

Etape 1 : Calculer la dérivée de la fonction

Etape 2 : Calculer le domaine de définition de la dérivée calculée à l'étape 1

[Tysse]

Du coup, pour calculer le domaine de définition de la dérivée, il y a des formules pour ça ? Ou alors on calcule comment ?
Car ce n'est absolument pas quelques choses que j'ai déjà vu en cours ...

[catamat]

Bonjour

En fait quand on dérive on applique un théorème qui impose parfois des conditions.

Ici au 1°) on a u/v : par théorème u/v est dérivable en tout point x où u et v sont dérivables et v(x) non nul.
Dans l'exemple u et v sont dérivable sur R et v ne s'annule pas sur l'intervalle proposé donc u/v est dérivable sur cet intervalle.

au 2°) on a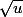 : par théorème 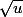est dérivable en tout point x où u est dérivable et u(x) > 0 (attention inégalité stricte !)
Dans l'exemple u est dérivable sur R mais n'est pas strictement positive sur l'intervalle proposé puisqu'elle s'annule en 1/2 donc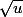 est dérivable sur ]1/2;+infini[

[Tysse]

Merci beaucoup je crois avoir compris !

[mathou13]

Bonjour,

F(x) existe si cos x # 0 <-> x#pi/2 +- pi donc est bien dérivable sur sont ensemble de definition

F(x) est dérivable si 4x-2>=0 <-> x>=1/2
Donc F est bien dérivable sur son ensemble de definition

[catamat]

F(x) est dérivable si 4x-2>=0 <-> x>=1/2
Donc F est bien dérivable sur son ensemble de definition

Désolé mais la fonction "racine carrée" n'est pas dérivable en 0 !
Donc F n'est pas dérivable en 1/2