Démonstration valeur absolue

[AntoinePinaye]

Bonsoir.
Je cherche à montrer que pour tous réels u, v : |u| + |v| ≤ |u+v| + |u−v|.
Could you help me ?
Merci

[mathelot]

bonjour,
élève les deux membres (positifs) de l'inégalité au carré:

[AntoinePinaye]

Merci de m'avoir répondue si tôt.
A-t-on le droit ? car |u| + |v| ≠ |u + v|^2

[Maxymyze]

Ne mélangeons pas tout.
Sur l'ensemble des réels > 0, a fonction x --> x^2 est strictement croissante, donc respecte strictement les inégalités.

[mathelot]

oui, élève au carré en utilisant l'identité
pour x et y réels

[catamat]

Bonjour

Une autre façon basique de voir la chose, en utilisant la définition de la somme des deux nombres (du moins une partie)

"Pour deux nombres de mêmes signes la valeur absolue de la somme est égale à la somme des valeurs absolues..."
donc dans ce cas |u|+|v|=|u+v|

et s'il sont de signes contraires alors u et (-v) sont de mêmes signes
donc dans ce cas |u|+|-v|=|u+(-v)| c'est à dire |u|+|v|=|u-v|

Dans les deux cas l'inégalité |u|+|v|<=|u+v|+|u-v| est vérifiée

On peut remarquer qu'il y a égalité si et seulement si u et v sont égaux ou opposés.

[mathelot]

méthode d'élévation au carré:


la fonction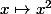 est strictement croissante sur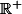
les assertions suivantes sont donc équivalentes:









Cette dernière inégalité est vraie. Cqfd.