Bonjour,
je dois démontrer par induction o les relations suivantes:
1)1+5+9+...+(4n-3)=n(2n-1) pour tout n>=1
2)1²+2²+...+n²=n(n+1)(2n+1)/6 pour tout n>=1
3)n³-n est divisible par 3 pour tout n>=1
4)1(1!),+2(2!)+...+n(n!)= (n+1)! pour tout n>=1
je suis complètement bloquée et ne sais pas par où commencer( (matière vue au cours lorsque j'étais absente). ext-ce que quelqu'un pourrait m'aider???
merci d'avance!
Démonstration pa récurrence
5 messages
- Page 1 sur 1
Re: démonstration pa récurrence
je dois démontrer par induction o les relations suivantes:
1)1+5+9+...+(4n-3)=n(2n-1) pour tout n>=1
tu regardes si c'est vrai pour n=1. (initialisation)
tu supposes que pour n fixé 1+5+9+...+(4n-3)=n(2n-1)
tu pars de la partie gauche, mais pour n+1
1+5+9+...+(4n-3)+(4(n+1)-3)
tu utilises le que l'on ait supposé 1+5+9+...+(4n-3)=n(2n-1)
reste donc à démontrer que c'est même chose que la partie droite au range n+1:
n(2n-1) +(4(n+1)-3) vaut-il bien (n+1)(2(n+1)-1) ?
finalement, tu as démontré que :
c'est vrai au départ
si c'est vrai pour un nombre n, c'est vrai aussi pour n+1
1)1+5+9+...+(4n-3)=n(2n-1) pour tout n>=1
tu regardes si c'est vrai pour n=1. (initialisation)
tu supposes que pour n fixé 1+5+9+...+(4n-3)=n(2n-1)
tu pars de la partie gauche, mais pour n+1
1+5+9+...+(4n-3)+(4(n+1)-3)
tu utilises le que l'on ait supposé 1+5+9+...+(4n-3)=n(2n-1)
reste donc à démontrer que c'est même chose que la partie droite au range n+1:
n(2n-1) +(4(n+1)-3) vaut-il bien (n+1)(2(n+1)-1) ?
finalement, tu as démontré que :
c'est vrai au départ
si c'est vrai pour un nombre n, c'est vrai aussi pour n+1
Re: démonstration pa récurrence
Bonjour;
Je vais expliciter la résolution du premier exercice par la méthode de récurrence ,
et tu vas essayer de l'appliquer pour les autres exercices .
Soit la proposition au rang
la proposition au rang 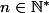 : "1 + 5 + 9 + ...... + (4n - 3) = n(2n - 1)" .
: "1 + 5 + 9 + ...... + (4n - 3) = n(2n - 1)" .
1)
Montrons que est vraie .
est vraie .
Pour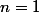 , on a :
, on a :  = 1) ; donc
; donc  est vraie .
est vraie .
2)
Supposons que pour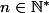 tel que
tel que  est vraie , montrons alors que
est vraie , montrons alors que 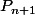 est vraie .
est vraie .
 est vraie , donc on a : 1 + 5 + 9 + ............. + (4n - 3) = n(2n - 1) ;
est vraie , donc on a : 1 + 5 + 9 + ............. + (4n - 3) = n(2n - 1) ;
donc : 1 + 5 + 9 + ............ + (4n - 3) + (4(n + 1) - 3) = n(2n - 1) + (4n + 1)
= 2n² - n + 4n + 1 = 2n² + 3n + 1 = 2n² + n + 2n + 1 = 2n(n + 1) + (n + 1)
= (n + 1)(2n + 1) = (n + 1)(2n + 2 - 1) = (n + 1)(2(n + 1) - 1) ; donc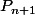 est vraie .
est vraie .
3)
On a montré que est vraie au rang
est vraie au rang 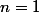 , et qu'elle est héréditaire,
, et qu'elle est héréditaire,
donc est vraie pour tout
est vraie pour tout 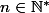 .
.
Je vais expliciter la résolution du premier exercice par la méthode de récurrence ,
et tu vas essayer de l'appliquer pour les autres exercices .
Soit
1)
Montrons que
Pour
2)
Supposons que pour
donc : 1 + 5 + 9 + ............ + (4n - 3) + (4(n + 1) - 3) = n(2n - 1) + (4n + 1)
= 2n² - n + 4n + 1 = 2n² + 3n + 1 = 2n² + n + 2n + 1 = 2n(n + 1) + (n + 1)
= (n + 1)(2n + 1) = (n + 1)(2n + 2 - 1) = (n + 1)(2(n + 1) - 1) ; donc
3)
On a montré que
donc
Modifié en dernier par aymanemaysae le 27 Nov 2018, 15:50, modifié 1 fois.
Re: démonstration pa récurrence
aymanemaysae a écrit:2)
Supposons qu'il existetel que
est vraie , montrons alors que
est vraie .
.
pour l'hérédité, on ne demande pas l'existence de n. En effet, il y a des propriétés qui sont héréditaires et toujours fausses
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
